
【題目】如圖,多面體![]() 中,四邊形
中,四邊形![]() 為矩形,二面角
為矩形,二面角![]() 為
為![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.

(1)求證:![]() 平面
平面![]() ;
;
(2)![]() 為線段
為線段![]() 上的點,當
上的點,當![]() 時,求二面角
時,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)證明見解析;(2)![]() .
.
【解析】
(1)根據四邊形![]() 是矩形,得到
是矩形,得到![]() ,根據線面平行的判定定理得到
,根據線面平行的判定定理得到![]() 平面
平面![]() ,進而得到
,進而得到![]() 平面
平面![]() ,利用面面平行的判定定理證得平面
,利用面面平行的判定定理證得平面![]() 平面
平面![]() ,利用面面平行的性質得到
,利用面面平行的性質得到![]() 平面
平面![]() ,證得結果;
,證得結果;
(2)根據題意,證得平面![]() 平面
平面![]() ,作
,作![]() 于點
于點![]() ,則
,則![]() 平面
平面![]() ,建立空間直角坐標系
,建立空間直角坐標系![]() ,寫出相應點的坐標,利用空間向量求得二面角的余弦值.
,寫出相應點的坐標,利用空間向量求得二面角的余弦值.
(1)證明:因為四邊形![]() 是矩形,所以
是矩形,所以![]() ,
,
又因為![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,
,
因為![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,
,
又因為![]() ,所以平面
,所以平面![]() 平面
平面![]() ,
,
而![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
(2)解:因為![]() ,
,![]() ,所以
,所以![]() ,
,
因為![]() 平面
平面![]() ,故平面
,故平面![]() 平面
平面![]() ,
,
作![]() 于點
于點![]() ,則
,則![]() 平面
平面![]() ,
,
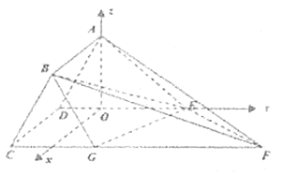
以![]() 為原點,平行于
為原點,平行于![]() 的直線為
的直線為![]() 軸,
軸,![]() 所在直線為
所在直線為![]() 軸,
軸,![]() 所在直線為
所在直線為![]() 軸,建立如圖所示的空間直角坐標系
軸,建立如圖所示的空間直角坐標系![]() ,
,
由![]() ,
,![]() ,
,![]() ,得
,得![]() ,
,![]() ,
,
則![]() ,
,![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,
由已知![]() ,所以
,所以![]() ,
,![]() ,
,
設平面![]() 的一個法向量為
的一個法向量為![]() ,則
,則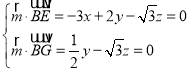 ,
,
取![]() ,
,![]() ,
,![]() ,得
,得![]() ,又平面
,又平面![]() 的一個法向量為
的一個法向量為![]() ,
,
所以![]() ,即二面角
,即二面角![]() 的余弦值為
的余弦值為![]() .
.


 優生樂園系列答案
優生樂園系列答案科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,傾斜角為
中,傾斜角為![]() 的直線
的直線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數).以坐標原點為極點,以
為參數).以坐標原點為極點,以![]() 軸的正半軸為極軸,建立極坐標系,曲線
軸的正半軸為極軸,建立極坐標系,曲線![]() 的極坐標方程是
的極坐標方程是![]() .
.
(Ⅰ)寫出直線![]() 的普通方程和曲線
的普通方程和曲線![]() 的直角坐標方程;
的直角坐標方程;
(Ⅱ)若直線![]() 經過曲線
經過曲線![]() 的焦點
的焦點![]() 且與曲線
且與曲線![]() 相交于
相交于![]() 兩點,設線段
兩點,設線段![]() 的中點為
的中點為![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某中學2018年的高考考生人數是2015年高考考生人數的![]() 倍,為了更好地對比該校考生的升學情況,統計了該校2015年和2018年的高考情況,得到如圖柱狀圖:
倍,為了更好地對比該校考生的升學情況,統計了該校2015年和2018年的高考情況,得到如圖柱狀圖:

則下列結論正確的是![]()
![]()
A. 與2015年相比,2018年一本達線人數減少
B. 與2015年相比,2018年二本達線人數增加了![]() 倍
倍
C. 2015年與2018年藝體達線人數相同
D. 與2015年相比,2018年不上線的人數有所增加
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】數學老師給出一個函數![]() ,甲、乙、丙、丁四個同學各說出了這個函數的一條性質:甲:在
,甲、乙、丙、丁四個同學各說出了這個函數的一條性質:甲:在![]() 上函數單調遞減;乙:在
上函數單調遞減;乙:在![]() 上函數單調遞增;丙:在定義域R上函數的圖象關于直線
上函數單調遞增;丙:在定義域R上函數的圖象關于直線![]() 對稱;丁:
對稱;丁:![]() 不是函數的最小值.老師說:你們四個同學中恰好有三個人說的正確.那么,你認為____說的是錯誤的.
不是函數的最小值.老師說:你們四個同學中恰好有三個人說的正確.那么,你認為____說的是錯誤的.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知某民族品牌手機生產商為迎合市場需求,每年都會研發推出一款新型號手機.該公司現研發了一款新型智能手機并投入生產,生產這款手機的月固定成本為80萬元,每生產1千臺,須另投入27萬元, 設該公司每月生產![]() 千臺并能全部銷售完,每1千臺的銷售收入為
千臺并能全部銷售完,每1千臺的銷售收入為![]() 萬元,且
萬元,且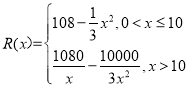 .為更好推廣該產品,手機生產商每月還支付各類廣告費用20萬元.
.為更好推廣該產品,手機生產商每月還支付各類廣告費用20萬元.
(Ⅰ)寫出月利潤![]() (萬元)關于月產量
(萬元)關于月產量![]() (千臺)的函數解析式;
(千臺)的函數解析式;
(Ⅱ)當月產量為多少千臺時,該公司在這一型號的手機生產中所獲月利潤最大?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 內,動點
內,動點![]() 到定點
到定點![]() 的距離與
的距離與![]() 到定直線
到定直線![]() 距離之比為
距離之比為![]() .
.
(Ⅰ)求動點![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(Ⅱ)設點![]() 是軌跡
是軌跡![]() 上兩個動點直線
上兩個動點直線![]() 與軌跡
與軌跡![]() 的另一交點分別為
的另一交點分別為![]() 且直線
且直線![]() 的斜率之積等于
的斜率之積等于![]() ,問四邊形
,問四邊形![]() 的面積
的面積![]() 是否為定值?請說明理由.
是否為定值?請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在三棱柱ABC—A1B1C1中,AA1=AC,A1B⊥AC1,設O為AC1與A1C的交點,點P為BC的中點.求證:
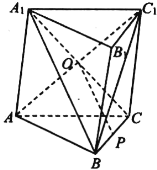
(1)OP∥平面ABB1A1;
(2)平面ACC1⊥平面OCP.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com