
【題目】某小型水庫的管理部門為研究庫區水量的變化情況,決定安排兩個小組在同一年中各自獨立的進行觀察研究.其中一個小組研究水源涵養情況.他們通過觀察入庫的若干小溪和降雨量等因素,隨機記錄了![]() 天的日入庫水量數據(單位:千
天的日入庫水量數據(單位:千![]() ),得到下面的柱狀圖(如圖甲).另一小組則研究由于放水、蒸發或滲漏造成的水量消失情況.他們通過觀察與水庫相連的特殊小池塘的水面下降情況來研究庫區水的整體消失量,隨機記錄了
),得到下面的柱狀圖(如圖甲).另一小組則研究由于放水、蒸發或滲漏造成的水量消失情況.他們通過觀察與水庫相連的特殊小池塘的水面下降情況來研究庫區水的整體消失量,隨機記錄了![]() 天的庫區日消失水量數據(單位:千
天的庫區日消失水量數據(單位:千![]() ),并將觀測數據整理成頻率分布直方圖(如圖乙).
),并將觀測數據整理成頻率分布直方圖(如圖乙).
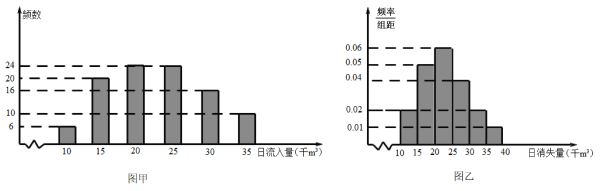
(1)據此估計這一年中日消失水量的平均值;
(2)以頻率作為概率,試解決如下問題:
①分別估計日流入水量不少于![]() 千
千![]() 和日消失量不多于
和日消失量不多于![]() 千
千![]() 的概率;
的概率;
②試估計經過一年后,該水庫的水量是增加了還是減少了,變化的量是多少?(一年按![]() 天計算),說明理由.
天計算),說明理由.
科目:高中數學 來源: 題型:
【題目】下列說法正確的是( )
A. 若命題![]() 均為真命題,則命題
均為真命題,則命題![]() 為真命題
為真命題
B. “若![]() ,則
,則![]() ”的否命題是“若
”的否命題是“若![]() ”
”
C. 在![]() ,“
,“![]() ”是“
”是“![]() ”的充要條件
”的充要條件
D. 命題![]() “
“![]() ”的否定為
”的否定為![]() “
“![]() ”
”
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知橢圓![]() :
:![]() 的離心率為
的離心率為![]() ,過左焦點
,過左焦點![]() 且斜率為
且斜率為![]() 的直線交橢圓
的直線交橢圓![]() 于
于![]() 兩點,線段
兩點,線段![]() 的中點為
的中點為![]() ,直線
,直線![]() :
:![]() 交橢圓
交橢圓![]() 于
于![]() 兩點.
兩點.
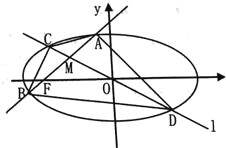
(1)求橢圓![]() 的方程;
的方程;
(2)求證:點![]() 在直線
在直線![]() 上;
上;
(3)是否存在實數![]() ,使得
,使得![]() ?若存在,求出
?若存在,求出![]() 的值,若不存在,說明理由.
的值,若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】隨著經濟的發展和個人收入的提高,自2018年10月1日起,個人所得稅起征點和稅率依法進行調整.調整如下:納稅人的工資、薪金所得,以每月全部收入額減5000元后的余額為應納稅所得額.依照個人所得稅稅率表,調整前后的計算方法如下表:
個人所得稅稅率表(調整前) | 個人所得稅稅率表(調整后) | ||||
免征額3500元 | 免征額5000元 | ||||
級數 | 全月應納稅所得額 | 稅率( | 級數 | 全月應納稅所得額 | 稅率( |
1 | 不超過1500元的部分 | 3 | 1 | 不超過3000元的部分 | 3 |
2 | 超過1500元至4500元的部分 | 10 | 2 | 超過3000元至12000元的部分 | 10 |
3 | 超過4500元至9000元的部分 | 20 | 3 | 超過12000元至25000元的部分 | 20 |
… | … | … | … | … | … |
(1)假如小李某月的工資、薪金等所得稅前收入為7500元時,請你幫小李算一下調整后小李的實際收入比調整前增加了多少?
(2)某稅務部門在小李所在公司利用分層抽樣方法抽取某月100個不同層次員工的稅前收入,并制成下面的頻數分布表:
收入 (元) |
|
|
|
|
|
|
人數 | 30 | 40 | 10 | 8 | 7 | 5 |
先從收入在![]() 及
及![]() 的人群中按分層抽樣抽取7人,再從中選4人作為新納稅法知識宣講員,用
的人群中按分層抽樣抽取7人,再從中選4人作為新納稅法知識宣講員,用![]() 表示抽到作為宣講員的收入在
表示抽到作為宣講員的收入在![]() 元的人數,
元的人數,![]() 表示抽到作為宣講員的收入在
表示抽到作為宣講員的收入在![]() 元的人數,隨機變量
元的人數,隨機變量![]() ,求
,求![]() 的分布列與數學期望.
的分布列與數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】國家規定每年的![]() 月
月![]() 日以后的
日以后的![]() 天為當年的暑假.某鋼琴培訓機構對
天為當年的暑假.某鋼琴培訓機構對![]() 位鋼琴老師暑假一天的授課量進行了統計,如下表所示:
位鋼琴老師暑假一天的授課量進行了統計,如下表所示:
授課量(單位:小時) |
|
|
|
|
|
頻數 |
|
|
|
|
|
培訓機構專業人員統計近![]() 年該校每年暑假
年該校每年暑假![]() 天的課時量情況如下表:
天的課時量情況如下表:
課時量(單位:天) |
|
|
|
|
|
頻數 |
|
|
|
|
|
(同組數據以這組數據的中間值作代表)
(1)估計![]() 位鋼琴老師一日的授課量的平均數;
位鋼琴老師一日的授課量的平均數;
(2)若以(1)中確定的平均數作為上述一天的授課量.已知當地授課價為![]() 元/小時,每天的各類生活成本為
元/小時,每天的各類生活成本為![]() 元/天;若不授課,不計成本,請依據往年的統計數據,估計一位鋼琴老師
元/天;若不授課,不計成本,請依據往年的統計數據,估計一位鋼琴老師![]() 天暑假授課利潤不少于
天暑假授課利潤不少于![]() 萬元的概率.
萬元的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設橢圓![]() 的左、右頂點分別為
的左、右頂點分別為![]() ,
,![]() ,上頂點為
,上頂點為![]() ,右焦點為
,右焦點為![]() ,已知
,已知![]() .
.
(1)證明:![]() .
.
(2)已知直線![]() 的傾斜角為
的傾斜角為![]() ,設
,設![]() 為橢圓
為橢圓![]() 上不同于
上不同于![]() ,
,![]() 的一點,
的一點,![]() 為坐標原點,線段
為坐標原點,線段![]() 的垂直平分線交
的垂直平分線交![]() 于
于![]() 點,過
點,過![]() 且垂直于
且垂直于![]() 的直線交
的直線交![]() 軸于
軸于![]() 點,若
點,若![]() ,求直線
,求直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在平面直角坐標系![]() 中,已知
中,已知![]() 兩點分別為橢圓
兩點分別為橢圓![]() 的右頂點和上頂點,且
的右頂點和上頂點,且![]() ,右準線
,右準線![]() 的方程為
的方程為![]() .
.

(1)求橢圓的標準方程;
(2)過點![]() 的直線交橢圓于另一點
的直線交橢圓于另一點![]() ,交
,交![]() 于點
于點![]() .若以
.若以![]() 為直徑的圓經過原點,求直線
為直徑的圓經過原點,求直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知直線y=k(x+1)(k>0)與拋物線C![]() 相交于A,B兩點,F為C的焦點,若|FA|=2|FB|,則|FA| =( )
相交于A,B兩點,F為C的焦點,若|FA|=2|FB|,則|FA| =( )
A.1B.2C.3D.4
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數,以坐標原點
為參數,以坐標原點![]() 為極點,
為極點,![]() 軸的正半軸為極軸,取相同長度單位建立極坐標系,曲線
軸的正半軸為極軸,取相同長度單位建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求曲線![]() 的極坐標方程和曲線
的極坐標方程和曲線![]() 的普通方程;
的普通方程;
(2)設射線![]() 與曲線
與曲線![]() 交于不同于極點的點
交于不同于極點的點![]() ,與曲線
,與曲線![]() 交于不同于極點的點
交于不同于極點的點![]() ,求線段
,求線段![]() 的長.
的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com