
| |||||||||||
(1) |
解析:由S1=a1=1.S2=a1+a2=1+a2,得t·(1+a2)-(2t+3)=3t. ∴a2= 又∵3tSn-(2t+3)Sn-1=3t, ① 3tSn-1-(2t+3)Sn-2=3t. ② ①-②得 3tan-(2t+3)an-1=0, ∴ 因此{an}為首項為1,公比為 |
(2) |
∵f(t)= ∴bn=f 故{bn}為一首項為1,公差為 ∴bn=1+ 點評:本題利用遞推公式證明{an}為等比數列時,一定要注意驗證從第2項起,即 |


 提分百分百檢測卷系列答案
提分百分百檢測卷系列答案科目:高中數學 來源:數學教研室 題型:044
3tSn-(2t+3)Sn-1=3t(t>0,n=2,3,4,…).
求證:數列{an}是等比數列;
查看答案和解析>>
科目:高中數學 來源:2012屆四川省成都外國語學校高三8月月考數學 題型:解答題
(本小題滿分12分)
設數列{an}的首項a1∈(0,1),an+1=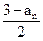 (n∈N+)
(n∈N+)
(I)求{an}的通項公式
(II)設bn=an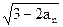 ,判斷數列{bn}的單調性,并證明你的結論
,判斷數列{bn}的單調性,并證明你的結論
查看答案和解析>>
科目:高中數學 來源:2011-2012學年四川省高三8月月考數學 題型:解答題
(本小題滿分12分)
設數列{an}的首項a1∈(0,1),an+1=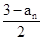 (n∈N+)
(n∈N+)
(I)求{an}的通項公式
(II)設bn=an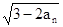 ,判斷數列{bn}的單調性,并證明你的結論
,判斷數列{bn}的單調性,并證明你的結論
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com