
【題目】已知橢圓![]() (a>b>0)的焦點在圓x2+y2=3上,且離心率為
(a>b>0)的焦點在圓x2+y2=3上,且離心率為![]() .
.
(Ⅰ)求橢圓C的方程;
(Ⅱ)過原點O的直線l與橢圓C交于A,B兩點,F為右焦點,若△FAB為直角三角形,求直線l的方程.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() 或
或![]() .
.
【解析】試題分析:(Ⅰ)由題意可得橢圓的焦點坐標,結合離心率,從而求出橢圓![]() 的方程;(Ⅱ)由
的方程;(Ⅱ)由![]() 為直角三角形,對
為直角三角形,對![]() 與
與![]() 是否垂直進行討論,從而分別求出直線
是否垂直進行討論,從而分別求出直線![]() 的方程.
的方程.
試題解析:(Ⅰ)因為橢圓的焦點在x軸上,所以焦點為圓x2+y2=3與x軸的交點,即![]() ,
, ![]() .
.
所以![]() .
.
又離心率![]() ,所以a=2.
,所以a=2.
故所求橢圓方程為![]() .
.
(Ⅱ)當△FAB為直角三角形時,顯然直線l斜率存在,
可設直線l方程為y=kx,設A(x1,y1),B(x2,y2).
(ⅰ)當FA⊥FB時, ![]() ,
, ![]() .
.
由![]()
消y得(4k2+1)x2-4=0.
則x1+x2=0, ![]() .
.
![]()
![]()
解得![]() .
.
此時直線l的方程為![]() .
.
(ⅱ)當FA與FB不垂直時,根據橢圓的對稱性,不妨設![]() .
.
所以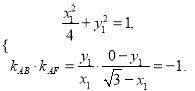 解得
解得
所以![]()
此時直線l的方程為![]() .
.
綜上,直線l的方程為![]() 或
或![]() .
.


 金牌教輔培優優選卷期末沖刺100分系列答案
金牌教輔培優優選卷期末沖刺100分系列答案科目:高中數學 來源: 題型:
【題目】動點P為橢圓 ![]() (a>b>0)上異于橢圓頂點A(a,0)、B(﹣a,0)的一點,F1 , F2為橢圓的兩個焦點,動圓M與線段F1P、F1F2的延長線級線段PF2相切,則圓心M的軌跡為除去坐標軸上的點的( )
(a>b>0)上異于橢圓頂點A(a,0)、B(﹣a,0)的一點,F1 , F2為橢圓的兩個焦點,動圓M與線段F1P、F1F2的延長線級線段PF2相切,則圓心M的軌跡為除去坐標軸上的點的( )
A.拋物線
B.橢圓
C.雙曲線的右支
D.一條直線
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,
, ![]() .
.
(1)求函數![]() 的最小正周期;
的最小正周期;
(2)若![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
【答案】(1) ![]() (2)
(2) ![]()
【解析】試題分析:(1)根據二倍角公式和兩角和差公式得到![]() ,進而得到周期;(2)由
,進而得到周期;(2)由![]() ,得到
,得到![]() ,
, ![]() ,由配湊角公式得到
,由配湊角公式得到![]() ,代入值得到函數值.
,代入值得到函數值.
解析:
(1)由題意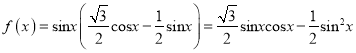
![]() =
=![]()
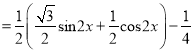
![]()
所以![]() 的最小正周期為
的最小正周期為![]() ;
;
(2)由![]()
![]()
又由![]() 得
得![]() ,所以
,所以![]()
故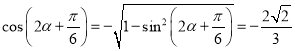 ,
,
故![]()
![]()
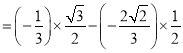
![]()
【題型】解答題
【結束】
20
【題目】為響應十九大報告提出的實施鄉村振興戰略,某村莊投資![]() 萬元建起了一座綠色農產品加工廠.經營中,第一年支出
萬元建起了一座綠色農產品加工廠.經營中,第一年支出![]() 萬元,以后每年的支出比上一年增加了
萬元,以后每年的支出比上一年增加了![]() 萬元,從第一年起每年農場品銷售收入為
萬元,從第一年起每年農場品銷售收入為![]() 萬元(前
萬元(前![]() 年的純利潤綜合=前
年的純利潤綜合=前![]() 年的 總收入-前
年的 總收入-前![]() 年的總支出-投資額
年的總支出-投資額![]() 萬元).
萬元).
(1)該廠從第幾年開始盈利?
(2)該廠第幾年年平均純利潤達到最大?并求出年平均純利潤的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 上的點到它的兩個焦的距離之和為
上的點到它的兩個焦的距離之和為![]() ,以橢圓
,以橢圓![]() 的短軸為直徑的圓
的短軸為直徑的圓![]() 經過這兩個焦點,點
經過這兩個焦點,點![]() ,
, ![]() 分別是橢圓
分別是橢圓![]() 的左、右頂點.
的左、右頂點.
(![]() )求圓
)求圓![]() 和橢圓
和橢圓![]() 的方程.
的方程.
(![]() )已知
)已知![]() ,
, ![]() 分別是橢圓
分別是橢圓![]() 和圓
和圓![]() 上的動點(
上的動點(![]() ,
, ![]() 位于
位于![]() 軸兩側),且直線
軸兩側),且直線![]() 與
與![]() 軸平行,直線
軸平行,直線![]() ,
, ![]() 分別與
分別與![]() 軸交于點
軸交于點![]() ,
, ![]() .求證:
.求證: ![]() 為定值.
為定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,已知圓O1與圓O2相交于A,B兩點,過點A作圓O1的切線交圓O2于點C,過點B作兩圓的割線,分別交圓O1 , 圓O2于點D,E,DE與AC相交于點P. 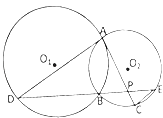
(1)求證:AD∥EC;
(2)若AD是圓O2的切線,且PA=3,PC=1,AD=6,求DB的長.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設實數x,y滿足不等式組  ,(2,1)是目標函數z=﹣ax+y取最大值的唯一最優解,則實數a的取值范圍是( )
,(2,1)是目標函數z=﹣ax+y取最大值的唯一最優解,則實數a的取值范圍是( )
A.(0,1)
B.(0,1]
C.(﹣∞,﹣2)
D.(﹣∞,﹣2]
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】解答
(1)在公比為2的等比數列{an}中,a2與a5的等差中項是9 ![]() .求a1的值;
.求a1的值;
(2)若函數y=a1sin( ![]() φ),0<φ<π的一部分圖象如圖所示,M(﹣1,a1),N(3,﹣a1)為圖象上的兩點,設∠MON=θ,其中O為坐標原點,0<θ<π,求cos(θ﹣φ)的值.
φ),0<φ<π的一部分圖象如圖所示,M(﹣1,a1),N(3,﹣a1)為圖象上的兩點,設∠MON=θ,其中O為坐標原點,0<θ<π,求cos(θ﹣φ)的值. 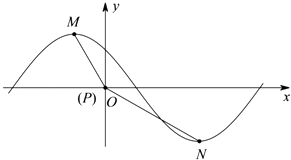
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某種出口產品的關稅稅率![]() ,市場價格
,市場價格![]() (單位:千元)與市場供應量
(單位:千元)與市場供應量![]() (單位:萬件)之間近似滿足關系式:
(單位:萬件)之間近似滿足關系式:![]() ,其中
,其中![]() 、
、![]() 均為常數.當關稅稅率為
均為常數.當關稅稅率為![]() 時,若市場價格為5千元,則市場供應量約為1萬件;當關稅稅率為
時,若市場價格為5千元,則市場供應量約為1萬件;當關稅稅率為![]() 時,若市場價格為7千元,則市場供應量約為2萬件.
時,若市場價格為7千元,則市場供應量約為2萬件.
(1)試確定![]() 、
、![]() 的值;
的值;
(2)市場需求量![]() (單位:萬件)與市場價格
(單位:萬件)與市場價格![]() 近似滿足關系式:
近似滿足關系式:![]() .當
.當![]() 時,市場價格稱為市場平衡價格.當市場平衡價格不超過4千元時,試確定關稅稅率的最大值.
時,市場價格稱為市場平衡價格.當市場平衡價格不超過4千元時,試確定關稅稅率的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】直線AB為圓的切線,切點為B,點C在圓上,∠ABC的角平分線BE交圓于點E,DB垂直BE交圓于點D. 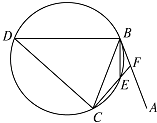
(1)證明:DB=DC;
(2)設圓的半徑為1,BC=3,延長CE交AB于點F,求△BCF外接圓的半徑.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com