
【題目】已知函數![]() ,(其中
,(其中![]() 為自然對數的底數).
為自然對數的底數).
(1)討論函數![]() 的單調性;
的單調性;
(2)當![]() 時,函數
時,函數![]() 有最小值
有最小值![]() ,求函數
,求函數![]() 的值域.
的值域.
【答案】(1)當![]() 時,
時,![]() 在
在![]() 上單調遞增;當
上單調遞增;當![]() 時,
時,![]() 在
在![]() 上單調遞減,
上單調遞減,![]() 在
在![]() 上單調遞增;(2)
上單調遞增;(2)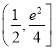 .
.
【解析】
(1)求出導數![]() ,分成
,分成![]() ,
,![]() 兩種情況求導數為零的根,從而可探究出函數和導數隨自變量的變化情況.
兩種情況求導數為零的根,從而可探究出函數和導數隨自變量的變化情況.
(2)求出![]() ,通過導數求出
,通過導數求出![]() 的單調性,結合零點存在定理得出存在
的單調性,結合零點存在定理得出存在![]() ,使得
,使得![]() ,即
,即![]() ,從而得出
,從而得出![]() 的單調性,進而求出
的單調性,進而求出![]() 的解析式,再利用
的解析式,再利用![]() 的單調性,從而可求其值域.
的單調性,從而可求其值域.
(1)解:![]() ,令
,令![]() ,當
,當![]() 時,
時,![]() 恒成立,此時
恒成立,此時![]() 單調遞增;
單調遞增;
當![]() 時,解
時,解![]() 得,
得,![]() ,則
,則![]() 隨
隨![]() 的變化如下表,
的變化如下表,
|
|
|
|
|
|
|
|
|
|
|
則![]() 在
在![]() 上遞減,
上遞減,![]() 在
在![]() 上遞增.
上遞增.
綜上所述,當![]() 時,
時,![]() 在
在![]() 上單調遞增;當
上單調遞增;當![]() 時,
時,![]() 在
在![]() 上單調遞減,
上單調遞減,![]() 在
在![]() 上單調遞增.
上單調遞增.
(2)因為![]() ,
,![]() ,則
,則![]() ,
,
則![]() ,設
,設![]() ,
,
則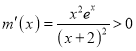 ,則
,則![]() 在
在![]() 上單調遞增.
上單調遞增.
對于![]() ,因為
,因為![]() ,
,![]() ,因此存在
,因此存在![]() ,
,
使得![]() ,即
,即![]() ,故
,故![]()
當![]() 時,
時,![]() ,
,![]() ,
,![]() 單調遞減;
單調遞減;
當![]() 時,
時,![]() ,
,![]() ,
,![]() 單調遞增.則
單調遞增.則![]()
即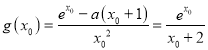 ,則
,則![]() ,由
,由 ,
,
可知,![]() 單調遞增.由
單調遞增.由![]() 得,
得,![]() .
.
所以![]() 的值域為
的值域為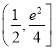 .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程為
的參數方程為![]() (
(![]() ,
,![]() 為參數),以坐標原點為極點,
為參數),以坐標原點為極點,![]() 軸的正半軸為極軸建立極坐標系,曲線
軸的正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)若![]() ,求
,求![]() 的極坐標方程;
的極坐標方程;
(2)若![]() 與
與![]() 恰有4個公共點,求
恰有4個公共點,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在正方體ABCD﹣A1B1C1D1中,E,F分別為B1C1,C1D1的中點,點P是上底面A1B1C1D1內一點,且AP∥平面EFDB,則cos∠APA1的最小值是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,四邊形![]() 是邊長為2的正方形.
是邊長為2的正方形.![]() 平面
平面![]() ,且
,且![]() .
.
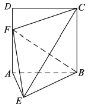
(1)求證:平面![]() 平面
平面![]() .
.
(2)線段![]() 上是否存在一點
上是否存在一點![]() ,使三棱錐
,使三棱錐![]() 的高
的高![]() 若存在,請求出
若存在,請求出![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2018年9月24日,阿貝爾獎和菲爾茲獎雙料得主、英國著名數學家阿蒂亞爵士宣布自己證明了黎曼猜想,這一事件引起了數學界的震動,在1859年,德國數學家黎曼向科學院提交了題目為《論小于某值的素數個數》的論文并提出了一個命題,也就是著名的黎曼猜想.在此之前,著名數學家歐拉也曾研究過這個問題,并得到小于數字![]() 的素數個數大約可以表示為
的素數個數大約可以表示為![]() 的結論(素數即質數,
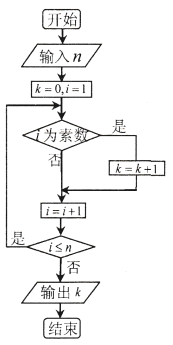
的結論(素數即質數,![]() ).根據歐拉得出的結論,如下流程圖中若輸入
).根據歐拉得出的結論,如下流程圖中若輸入![]() 的值為
的值為![]() ,則輸出
,則輸出![]() 的值應屬于區間( )
的值應屬于區間( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線![]() ,過點
,過點![]() 的直線
的直線![]() 與
與![]() 交于不同的兩點
交于不同的兩點![]() ,且滿足
,且滿足![]() ,以
,以![]() 為中點的線段的兩端點分別為
為中點的線段的兩端點分別為![]() ,其中
,其中![]() 在
在![]() 軸上,
軸上,![]() 在
在![]() 上,則
上,則![]() _______,
_______,![]() 的最小值為____________
的最小值為____________
查看答案和解析>>
科目:高中數學 來源: 題型:
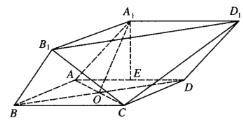
【題目】由四棱柱![]() 截去三棱錐
截去三棱錐![]() 后得到的幾何體如圖所示,四邊形
后得到的幾何體如圖所示,四邊形![]() 是邊長為
是邊長為![]() 的正方形,
的正方形,![]() 為
為![]() 與
與![]() 的交點,
的交點,![]() 為
為![]() 的中點,
的中點,![]() 平面
平面![]() .
.
(Ⅰ)證明:![]() 平面
平面![]() ;
;
(Ⅱ)若直線![]() 與平面
與平面![]() 所成的角為
所成的角為![]() ,求線段
,求線段![]() 的長.
的長.
查看答案和解析>>
科目:高中數學 來源: 題型:
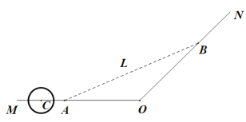
【題目】為解決城市的擁堵問題,某城市準備對現有的一條穿城公路MON進行分流,已知穿城公路MON自西向東到達城市中心點O后轉向東北方向(即![]() ).現準備修建一條城市高架道路L,L在MO上設一出入口A,在ON上設一出入口B.假設高架道路L在AB部分為直線段,且要求市中心O與AB的距離為10km.
).現準備修建一條城市高架道路L,L在MO上設一出入口A,在ON上設一出入口B.假設高架道路L在AB部分為直線段,且要求市中心O與AB的距離為10km.
(1)求兩站點A,B之間距離的最小值;
(2)公路MO段上距離市中心O30km處有一古建筑群C,為保護古建筑群,設立一個以C為圓心,5km為半徑的圓形保護區.則如何在古建筑群C和市中心O之間設計出入口A,才能使高架道路L及其延伸段不經過保護區(不包括臨界狀態)?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com