【題目】在①函數
為奇函數；②當
時，
；③
是函數
的一個零點這三個條件中任選一個，補充在下面問題中，并解答，已知函數
，的圖象相鄰兩條對稱軸間的距離為
，______.
（1）求函數的解析式；
（2）求函數在
上的單調遞增區間.
【答案】（1）選條件①②③任一個，均有
；（2）選條件①②③任一個，函數
在
上的單調遞增區間均為
，
.
【解析】
（1）由相鄰兩條對稱軸間的距離為
，得到
；再選擇一個條件求解出
；
（2）由（1）解得的函數，根據復合函數的單調性得到單調區間.
解： 
函數的圖象相鄰對稱軸間的距離為，
，
，
.
方案一：選條件①
為奇函數，
，
解得：
，
.
（1）
，
，
；
（2）由
，，
得
，，
令
，得
，令
，得
，
函數在上的單調遞增區間為，；
方案二：選條件②
，
，
，或
，，
（1），，；
（2）由，，
得，，
令，得，令，得，
函數在上的單調遞增區間為，；
方案三：選條件③
是函數的一個零點，
，
，.
（1），，；
（2）由，，得，
令，得，令，得.
函數在上的單調遞增區間為，
閱讀快車系列答案科目：高中數學 來源： 題型：
【題目】如圖所示，圖①是棱長為1的小正方體，圖②，③是由這樣的小正方體擺放而成．按照這樣的方法繼續擺放，由上而下分別將第1層，第2層，…，第
層的小正方體的個數記為
，解答下列問題：
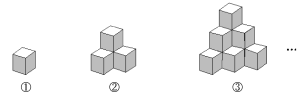
（1）按照要求填表：
| 1 | 2 | 3 | 4 | … |
| 1 | 3 | 6 | _ | … |
（2）
__________．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】【選修4-4：坐標系與參數方程】
在直角坐標系
中，曲線
的參數方程為
（
為參數），以坐標原點
為極點，
軸的正半軸為極軸建立極坐標系，曲線
的極坐標方程為
.
（Ⅰ）求曲線
的極坐標方程和
的直角坐標方程；
（Ⅱ）直線
與曲線
分別交于第一象限內的
，
兩點，求
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】若AC⊥BC，AC=BC=1，點P是△ABC內一點，則
的取值范圍是（ ）
A. （﹣
，0） B. （0，） C. （﹣，） D. （﹣1，1）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】若一個函數當自變量在不同范圍內取值時，函數表達式不同，我們稱這樣的函數為分段函數．下面我們參照學習函數的過程與方法，探究分段函數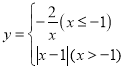
的圖象與性質．列表：
x | … |
|
|
|
|
|
| 0 |
| 1 |
| 2 |
| 3 | … |
y | … |
|
| 1 |
| 2 |
| 1 |
| 0 |
| 1 |
| 2 | … |
描點：在平面直角坐標系中，以自變量x的取值為橫坐標，以相應的函數值y為縱坐標，描出相應的點，如圖所示．
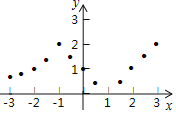
（1）如圖，在平面直角坐標系中，觀察描出的這些點的分布，作出函數圖象；
（2）研究函數并結合圖象與表格，回答下列問題：
①點
，
，
，
在函數圖象上，
，
；（填“＞”，“＝”或“＜”）
②當函數值
時，求自變量x的值；
③在直線
的右側的函數圖象上有兩個不同的點
，
，且
，求
的值；
④若直線
與函數圖象有三個不同的交點，求a的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】“楊輝三角”是我國數學史上的一個偉大成就，是二項式系數在三角形中的一種幾何排列.如圖所示，去除所有為1的項，依此構成數列2，3，3，4，6，4，5，10，10，5，…，則此數列的前56項和為_____.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】圖是A，B兩所學校藝術節期間收到的各類藝術作品的情況的統計圖：
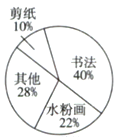
A學校 B學校
（1）從圖中能否看出哪所學校收到的水粉畫作品數量多？為什么？
（2）已知A學校收到的剪紙作品比B學校的多20件，收到的書法作品比B學校的少100件，請問這兩所學校收到藝術作品的總數分別是多少件？
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
