
【題目】已知函數![]()
![]() .
.
(1)當![]() 時,求函數
時,求函數![]() 在點
在點![]() 處的切線方程.
處的切線方程.
(2)求函數![]() 的單調區間.
的單調區間.
【答案】(1)![]() ;(2)見解析.
;(2)見解析.
【解析】試題分析:
(1)函數的定義域![]() ,當
,當![]() 時,計算可得:
時,計算可得:![]() ,
,![]() ,則切線方程為
,則切線方程為![]() .
.
(2)![]() ,考查二次函數
,考查二次函數![]() ,分類討論:
,分類討論:
①若![]() ,
,![]() 在
在![]() 上單調遞增,在
上單調遞增,在![]() 上單調遞減.
上單調遞減.
②若![]() ,
,![]() 為開口向上的二次函數,兩個零點均在定義域
為開口向上的二次函數,兩個零點均在定義域![]() 上.則:
上.則:
(i)若![]() ,函數
,函數![]() 在
在![]() 和
和![]() 上單調遞增,在
上單調遞增,在![]() 上單調遞減.
上單調遞減.
(ii)若![]() ,
,![]() 在
在![]() 上單調遞增.
上單調遞增.
(iii)若![]() ,函數
,函數![]() 在
在![]() 和
和![]() 上單調遞增,在
上單調遞增,在![]() 上單調遞減.
上單調遞減.
試題解析:
(1)函數的定義域![]() ,
,
當![]() 時,
時,![]() ,
,![]() ,
,
![]() ,∴切線方程為
,∴切線方程為![]() .
.
(2)![]() ,
,
易知![]() ,令
,令![]() ,
,
①若![]() ,
,![]() ,∴
,∴![]() 在
在![]() 上單調遞增,在
上單調遞增,在![]() 上單調遞減.
上單調遞減.
②若![]() ,
,![]() 為開口向上的二次函數,零點分別為0,
為開口向上的二次函數,零點分別為0,![]() ,其中
,其中![]() ,
,
即![]() 的兩個零點均在定義域
的兩個零點均在定義域![]() 上.
上.
(i)若![]() ,
,![]() ,所以函數
,所以函數![]() 在
在![]() 和
和![]() 上單調遞增,在
上單調遞增,在![]() 上單調遞減.
上單調遞減.
(ii)若![]() ,
,![]() ,
,![]() 圖象恒在
圖象恒在![]() 軸上方,
軸上方,![]() 恒成立,∴
恒成立,∴![]() 在
在![]() 上單調遞增.
上單調遞增.
(iii)若![]() ,
,![]() ,∴函數
,∴函數![]() 在
在![]() 和
和![]() 上單調遞增,在
上單調遞增,在![]() 上單調遞減.
上單調遞減.


科目:高中數學 來源: 題型:
【題目】已知橢圓C:![]() (a>b>0)的兩個焦點分別為F1,F2,離心率為
(a>b>0)的兩個焦點分別為F1,F2,離心率為![]() ,過F1的直線l與橢圓C交于M,N兩點,且△MNF2的周長為8.
,過F1的直線l與橢圓C交于M,N兩點,且△MNF2的周長為8.
(1)求橢圓C的方程;
(2)若直線y=kx+b與橢圓C分別交于A,B兩點,且OA⊥OB,試問點O到直線AB的距離是否為定值,證明你的結論.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在①函數![]() 為奇函數;②當
為奇函數;②當![]() 時,
時,![]() ;③
;③![]() 是函數
是函數![]() 的一個零點這三個條件中任選一個,補充在下面問題中,并解答,已知函數
的一個零點這三個條件中任選一個,補充在下面問題中,并解答,已知函數![]() ,
,![]() 的圖象相鄰兩條對稱軸間的距離為
的圖象相鄰兩條對稱軸間的距離為![]() ,______.
,______.
(1)求函數![]() 的解析式;
的解析式;
(2)求函數![]() 在
在![]() 上的單調遞增區間.
上的單調遞增區間.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】探究函數![]() 的圖象與性質.
的圖象與性質.
(1)下表是y與x的幾組對應值.
| … |
|
|
|
|
|
|
| … |
| … |
|
|
|
|
|
|
| … |
其中m的值為_______________;
(2)根據上表數據,在如圖所示的平面直角坐標系中描點,并已畫出了函數圖象的一部分,請你畫出該圖象的另一部分;

(3)結合函數的圖象,寫出該函數的一條性質:_________;
(4)若關于x的方程![]() 有2個實數根,則t的取值范圍是______.
有2個實數根,則t的取值范圍是______.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】![]() 年春節期間,某服裝超市舉辦了一次有獎促銷活動,消費每超過
年春節期間,某服裝超市舉辦了一次有獎促銷活動,消費每超過![]() 元(含
元(含![]() 元),均可抽獎一次,抽獎方案有兩種,顧客只能選擇其中的一種.方案一:從裝有
元),均可抽獎一次,抽獎方案有兩種,顧客只能選擇其中的一種.方案一:從裝有![]() 個形狀、大小完全相同的小球(其中紅球
個形狀、大小完全相同的小球(其中紅球![]() 個,黑球
個,黑球![]() 個)的抽獎盒中,一次性摸出
個)的抽獎盒中,一次性摸出![]() 個球,其中獎規則為:若摸到
個球,其中獎規則為:若摸到![]() 個紅球,享受免單優惠;若摸出
個紅球,享受免單優惠;若摸出![]() 個紅球則打
個紅球則打![]() 折,若摸出
折,若摸出![]() 個紅球,則打
個紅球,則打![]() 折;若沒摸出紅球,則不打折.方案二:從裝有
折;若沒摸出紅球,則不打折.方案二:從裝有![]() 個形狀、大小完全相同的小球(其中紅球
個形狀、大小完全相同的小球(其中紅球![]() 個,黑球
個,黑球![]() 個)的抽獎盒中,有放回每次摸取
個)的抽獎盒中,有放回每次摸取![]() 球,連摸
球,連摸![]() 次,每摸到
次,每摸到![]() 次紅球,立減
次紅球,立減![]() 元.
元.
(1)若兩個顧客均分別消費了![]() 元,且均選擇抽獎方案一,試求兩位顧客均享受免單優惠的概率;
元,且均選擇抽獎方案一,試求兩位顧客均享受免單優惠的概率;
(2)若某顧客消費恰好滿![]() 元,試從概率的角度比較該顧客選擇哪一種抽獎方案更合算?
元,試從概率的角度比較該顧客選擇哪一種抽獎方案更合算?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,某地有南北街道5條,東西街道5條,現在甲、乙、丙3名郵遞員從該地西南角的郵局![]() 出發,送信到東北角的
出發,送信到東北角的![]() 地,要求所走路程最短,設圖中點
地,要求所走路程最短,設圖中點![]() ,
,![]() ,
,![]() 是交叉路口,且
是交叉路口,且![]() 路段由于修路不能通行.
路段由于修路不能通行.
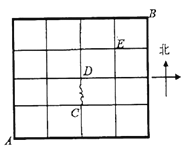
(1)求甲從![]() 到
到![]() 共有多少種走法?(用數字作答)
共有多少種走法?(用數字作答)
(2)求甲經過點![]() 的概率;
的概率;
(3)設3名郵遞員恰有![]() 名郵遞員經過點
名郵遞員經過點![]() ,求隨機變量
,求隨機變量![]() 的概率分布和數學期望.
的概率分布和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
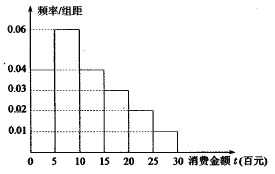
【題目】“雙十一”已經成為網民們的網購狂歡節,某電子商務平臺對某市的網民在今年“雙十一”的網購情況進行摸底調查,用隨機抽樣的方法抽取了100人,其消費金額![]() (百元)的頻率分布直方圖如圖所示:
(百元)的頻率分布直方圖如圖所示:
(1)求網民消費金額![]() 的平均值和中位數
的平均值和中位數![]() ;
;
(2)把下表中空格里的數填上,能否有![]() 的把握認為網購消費與性別有關;
的把握認為網購消費與性別有關;
男 | 女 | 合計 | |
| |||
| 30 | ||
合計 | 45 |
附表:
|
|
|
|
|
|
|
|
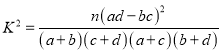 .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“微信運動”已成為當下熱門的健身方式,小王的微信朋友圈內也有大量好友參與了“微信運動”,他隨機選取了其中的![]() 人(男、女各
人(男、女各![]() 人),記錄了他們某一天的走路步數,并將數據整理如下:
人),記錄了他們某一天的走路步數,并將數據整理如下:
步量 性別 | 0~2000 | 2001~5000 | 5001~8000 | 8001~10000 | >10000 |
男 | 1 | 2 | 3 | 6 | 8 |
女 | 0 | 2 | 10 | 6 | 2 |
(1)已知某人一天的走路步數超過![]() 步被系統評定“積極型”,否則為“懈怠型”,根據題意完成下面的
步被系統評定“積極型”,否則為“懈怠型”,根據題意完成下面的![]() 列聯表,并據此判斷能否有
列聯表,并據此判斷能否有![]() 以上的把握認為“評定類型”與“性別”有關?
以上的把握認為“評定類型”與“性別”有關?
積極型 | 懈怠型 | 總計 | |
男 | |||
女 | |||
總計 |
附:![]() ,
,
| 0.10 | 0.05 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
(2)若小王以這![]() 位好友該日走路步數的頻率分布來估計其所有微信好友每日走路步數的概率分布,現從小王的所有微信好友中任選
位好友該日走路步數的頻率分布來估計其所有微信好友每日走路步數的概率分布,現從小王的所有微信好友中任選![]() 人,其中每日走路不超過
人,其中每日走路不超過![]() 步的有
步的有![]() 人,超過
人,超過![]() 步的有
步的有![]() 人,設
人,設![]() ,求
,求![]() 的分布列及數學期望.
的分布列及數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】給出下面類比推理:
①“若2a<2b,則a<b”類比推出“若a2<b2,則a<b”;
②“(a+b)c=ac+bc(c≠0)”類比推出“![]() (c≠0)”;
(c≠0)”;
③“a,b∈R,若a-b=0,則a=b”類比推出“a,b∈C,若a-b=0,則a=b”;
④“a,b∈R,若a-b>0,則a>b”類比推出“a,b∈C,若a-b>0,則a>b(C為復數集)”.
其中結論正確的個數為( )
A. 1B. 2C. 3D. 4
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com