
【題目】已知函數![]() ,
,![]() ,令
,令![]()
(1)當![]() 時,求函數
時,求函數![]() 的單調區間;
的單調區間;
(2)若關于![]() 的不等式
的不等式![]() 恒成立,求整數
恒成立,求整數![]() 的最小值.
的最小值.
【答案】(1)![]() 的單調遞增區間為
的單調遞增區間為![]() ,單調遞減區間為
,單調遞減區間為![]() .
.
(2)![]()
【解析】
(1)先求函數的定義域,然后求導,通過導數大于零得到增區間;
(2)不等式恒成立問題轉化為函數的最值問題,應先求導數,研究函數的單調性,然后求函數的最值;
解:(1)當![]() 時,
時,![]()
![]() .
.
令![]() 得
得![]() 又
又![]() ,所以
,所以![]() .所以
.所以![]() 的單調遞增區間為
的單調遞增區間為![]() .
.
令![]() 得
得![]() 又
又![]() ,所以
,所以![]() .所以
.所以![]() 的單調遞減區間為
的單調遞減區間為![]() .
.
綜上可得:![]() 的單調遞增區間為
的單調遞增區間為![]() ,單調遞減區間為
,單調遞減區間為![]() .
.
(2)令![]() .
.
所以![]() .
.
當![]() 時,因為
時,因為![]() ,所以
,所以![]() 所以
所以![]() 在
在![]() 上是遞增函數,
上是遞增函數,
又因為![]() .
.
所以關于![]() 的不等式
的不等式![]() 不能恒成立.
不能恒成立.
當![]() 時,
時,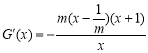 .
.
令![]() 得
得![]() ,所以當
,所以當![]() 時,
時,![]() ;當
;當![]() 時,
時,![]() .
.
因此函數![]() 在
在![]() 是增函數,在
是增函數,在![]() 是減函數.
是減函數.
故函數![]() 的最大值為
的最大值為![]() .
.
令![]() ,因為
,因為![]() ,
,![]() .
.
又因為![]() 在
在![]() 上是減函數,所以當
上是減函數,所以當![]() 時,
時,![]() .
.
所以整數![]() 的最小值為2.
的最小值為2.


科目:高中數學 來源: 題型:
【題目】為了解甲、乙兩個快遞公司的工作狀況,假設同一個公司快遞員的工作狀況基本相同,現從甲、乙兩公司各隨機抽取一名快遞員,并從兩人某月(30天)的快遞件數記錄結果中隨機抽取10天的數據,整理如下:
甲公司員工![]() :410,390,330,360,320,400,330,340,370,350
:410,390,330,360,320,400,330,340,370,350
乙公司員工![]() :360,420,370,360,420,340,440,370,360,420
:360,420,370,360,420,340,440,370,360,420
每名快遞員完成一件貨物投遞可獲得的勞務費情況如下:甲公司規定每件0.65元,乙公司規定每天350件以內(含350件)的部分每件0.6元,超出350件的部分每件0.9元.
(1)根據題中數據寫出甲公司員工![]() 在這10天投遞的快件個數的平均數和眾數;
在這10天投遞的快件個數的平均數和眾數;
(2)為了解乙公司員工![]() 每天所得勞務費的情況,從這10天中隨機抽取1天,他所得的勞務費記為
每天所得勞務費的情況,從這10天中隨機抽取1天,他所得的勞務費記為![]() (單位:元),求
(單位:元),求![]() 的分布列和數學期望;
的分布列和數學期望;
(3)根據題中數據估算兩公司被抽取員工在該月所得的勞務費.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,
中,![]() 的參數方程為
的參數方程為 (t為參數).以坐標原點O為極點,x軸的正半軸為極軸建立極坐標系,曲線C的極坐標方程為
(t為參數).以坐標原點O為極點,x軸的正半軸為極軸建立極坐標系,曲線C的極坐標方程為![]() .
.
(1)求![]() 的普通方程和曲線C的直角坐標方程;
的普通方程和曲線C的直角坐標方程;
(2)求曲線C上的點到![]() 距離的最大值及該點坐標.
距離的最大值及該點坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
:![]() 的左、右頂點分別為C、D,且過點
的左、右頂點分別為C、D,且過點![]() ,P是橢圓上異于C、D的任意一點,直線PC,PD的斜率之積為
,P是橢圓上異于C、D的任意一點,直線PC,PD的斜率之積為![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)O為坐標原點,設直線CP交定直線x = m于點M,當m為何值時,![]() 為定值.
為定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】秦九韶是我國南宋時期的數學家,普州(現四川省安岳縣)人,他在所著的《數書九章》中提出的多項式求值的秦九韶算法,至今仍是比較先進的算法,如圖所示的程序框圖,給出了利用秦九韶算法求某多項式值的一個實例,若輸入x的值為2,則輸出![]() 的值為( )
的值為( )
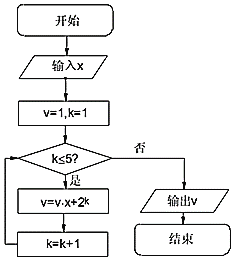
A.80B.192C.448D.36
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com