【題目】甲、乙兩人在相同條件下各射擊
次，每次中靶環數情況如圖所示：
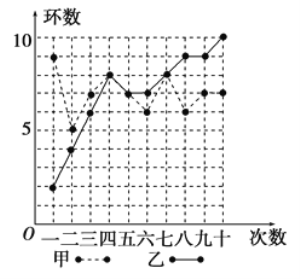
（1）請填寫下表（先寫出計算過程再填表）：
平均數 | 方差 | 命中 | |
甲 |
|
|
|
乙 |
（2）從下列三個不同的角度對這次測試結果進行
①從平均數和方差相結合看（分析誰的成績更穩定）；
②從平均數和命中
環及環以上的次數相結合看（分析誰的成績好些）；
③從折線圖上兩人射擊命中環數的走勢看（分析誰更有潛力）.
【答案】（1）填表見解析；（2）①甲成績比乙穩定；②乙成績比甲好些；③乙更有潛力.
【解析】
（1）由拆線圖，求出
和
，完成列聯表．
（2）①平均數相同，
，從而甲成績比乙穩定．
②平均數相同，命中9環及9環以上的次數甲比乙少，乙成績比甲好些．
③甲成績在平均數上下波動；而乙處于上升勢頭，從第三次以后就沒有比甲少的情況發生，乙更有潛力．
解：由列聯表中數據，計算由題圖，知：
甲射擊10次中靶環數分別為9，5，7，8，7，6，8，6，7，7．
將它們由小到大排列為5，6，6，7，7，7，7，8，8，9．
乙射擊10次中靶環數分別為2，4，6，8，7，7，8，9，9，10．
將它們由小到大排列為2，4，6，7，7，8，8，9，9，10．
（1）
（環
，
．
填表如下：
平均數 | 方差 | 命中9環及9環以上的次數 | |
甲 | 7 | 1.2 | 1 |
乙 | 7 | 5.4 | 3 |
（2）①
平均數相同，，
甲成績比乙穩定．
②平均數相同，命中9環及9環以上的次數甲比乙少，乙成績比甲好些．
③甲成績在平均數上下波動；而乙處于上升勢頭，從第三次以后就沒有比甲少的情況發生，乙更有潛力．
名校課堂系列答案科目：高中數學 來源： 題型：
【題目】某醫療器械公司在全國共有
個銷售點，總公司每年會根據每個銷售點的年銷量進行評價分析.規定每個銷售點的年銷售任務為一萬四千臺器械.根據這個銷售點的年銷量繪制出如下的頻率分布直方圖.
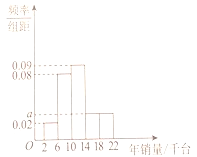
（1）完成年銷售任務的銷售點有多少個？
（2）若用分層抽樣的方法從這個銷售點中抽取容量為
的樣本，求該五組
，
，
，
，
，（單位：千臺）中每組分別應抽取的銷售點數量.
（3）在（2）的條件下，從該樣本中完成年銷售任務的銷售點中隨機選取
個，求這兩個銷售點不在同一組的概率.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】汽車的“燃油效率”是指汽車每消耗1升汽油行駛的里程，下圖描述了甲、乙、丙三輛汽車在不同速度下的燃油效率情況.下列敘述中正確的是（ ）
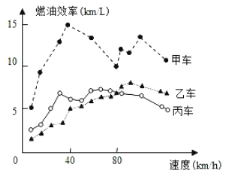
A.消耗1升汽油，乙車最多可行駛5千米
B.以相同速度行駛相同路程，三輛車中，甲車消耗汽油最多
C.甲車以80千米/小時的速度行駛1小時，消耗8升汽油
D.某城市機動車最高限速80千米/小時.相同條件下，在該市用乙車比用丙車更省油
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在平面直角坐標系
中，已知點
，圓
：
與
軸的正半軸的交點是
，過點
的直線
與圓交于不同的兩點
.
（1）若直線與
軸交于
，且
，求直線的方程；
（2）設直線
，
的斜率分別是
，
，求
的值；
（3）設
的中點為
，點
，若
，求
的面積.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知數列{an}滿足a1＝1， 
，其中n∈N*．
（1）設
，求證：數列{bn}是等差數列，并求出{an}的通項公式．
（2）設
，數列{cncn+2}的前n項和為Tn，是否存在正整數m，使得
對于n∈N*，恒成立？若存在，求出m的最小值；若不存在，請說明．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】近年來，共享單車已經悄然進入了廣大市民的日常生活，并慢慢改變了人們的出行方式.為了更好地服務民眾，某共享單車公司在其官方
中設置了用戶評價反饋系統，以了解用戶對車輛狀況和優惠活動的評價.現從評價系統中選出
條較為詳細的評價信息進行統計，車輛狀況的優惠活動評價的
列聯表如下：
對優惠活動好評 | 對優惠活動不滿意 | 合計 | |
對車輛狀況好評 |
|
|
|
對車輛狀況不滿意 |
|
|
|
合計 |
|
|
|
（1）能否在犯錯誤的概率不超過
的前提下認為優惠活動好評與車輛狀況好評之間有關系？
（2）為了回饋用戶，公司通過向用戶隨機派送騎行券.用戶可以將騎行券用于騎行付費，也可以通過轉贈給好友.某用戶共獲得了
張騎行券，其中只有
張是一元券.現該用戶從這張騎行券中隨機選取張轉贈給好友，求選取的張中至少有
張是一元券的概率.
參考數據：
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
參考公式：
，其中
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
