
【題目】已知橢圓![]() :
:![]() 的左、右焦點(diǎn)分別為
的左、右焦點(diǎn)分別為![]() ,
,![]() ,焦距為2,且經(jīng)過(guò)點(diǎn)
,焦距為2,且經(jīng)過(guò)點(diǎn)![]() ,斜率為
,斜率為![]() 的直線
的直線![]() 經(jīng)過(guò)點(diǎn)
經(jīng)過(guò)點(diǎn)![]() ,與橢圓
,與橢圓![]() 交于
交于![]() ,
,![]() 兩點(diǎn).
兩點(diǎn).
(1)求橢圓![]() 的方程;
的方程;
(2)在![]() 軸上是否存在點(diǎn)
軸上是否存在點(diǎn)![]() ,使得以
,使得以![]() ,
,![]() 為鄰邊的平行四邊形是菱形?如果存在,求出
為鄰邊的平行四邊形是菱形?如果存在,求出![]() 的取值范圍,如果不存在,請(qǐng)說(shuō)明理由.
的取值范圍,如果不存在,請(qǐng)說(shuō)明理由.
【答案】(1)![]() (2)存在;實(shí)數(shù)
(2)存在;實(shí)數(shù)![]() 的取值范圍是
的取值范圍是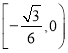
【解析】
(1)根據(jù)橢圓定義計(jì)算![]() ,再根據(jù)
,再根據(jù)![]() ,
,![]() ,
,![]() 的關(guān)系計(jì)算
的關(guān)系計(jì)算![]() 即可得出橢圓方程;(2)設(shè)直線
即可得出橢圓方程;(2)設(shè)直線![]() 方程為
方程為![]() ,與橢圓方程聯(lián)立方程組,求出
,與橢圓方程聯(lián)立方程組,求出![]() 的范圍,根據(jù)根與系數(shù)的關(guān)系求出
的范圍,根據(jù)根與系數(shù)的關(guān)系求出![]() 的中點(diǎn)坐標(biāo),求出
的中點(diǎn)坐標(biāo),求出![]() 的中垂線與
的中垂線與![]() 軸的交點(diǎn)橫,得出
軸的交點(diǎn)橫,得出![]() 關(guān)于
關(guān)于![]() 的函數(shù),利用基本不等式得出
的函數(shù),利用基本不等式得出![]() 的范圍.
的范圍.
(1)由題意可知![]() ,
,![]() ,
,![]() .
.
又![]() ,
,
![]() ,
,![]() ,
,
![]() 橢圓
橢圓![]() 的方程為:
的方程為:![]() .
.
(2)若存在點(diǎn)![]() ,使得以
,使得以![]() ,
,![]() 為鄰邊的平行四邊形是菱形,
為鄰邊的平行四邊形是菱形,
則![]() 為線段
為線段![]() 的中垂線與
的中垂線與![]() 軸的交點(diǎn).
軸的交點(diǎn).
設(shè)直線![]() 的方程為:
的方程為:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
聯(lián)立方程組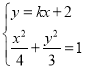 ,消元得:
,消元得:![]() ,
,
△![]() ,又
,又![]() ,故
,故![]() .
.
由根與系數(shù)的關(guān)系可得![]() ,設(shè)
,設(shè)![]() 的中點(diǎn)為
的中點(diǎn)為![]() ,
,![]() ,
,
則![]() ,
,![]() ,
,
![]() 線段
線段![]() 的中垂線方程為:
的中垂線方程為:![]() ,
,
令![]() 可得
可得 ,即
,即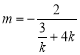 .
.
![]() ,故
,故![]() ,當(dāng)且僅當(dāng)
,當(dāng)且僅當(dāng)![]() 即
即![]() 時(shí)取等號(hào),
時(shí)取等號(hào),
![]() ,且
,且![]() .
.
![]() 的取值范圍是
的取值范圍是![]() ,
,![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學(xué)生10分鐘應(yīng)用題系列答案
小學(xué)生10分鐘應(yīng)用題系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】第七屆世界軍人運(yùn)動(dòng)會(huì)于2019年10月18日至27日在中國(guó)武漢舉行,中國(guó)隊(duì)以133金64銀42銅位居金牌榜和獎(jiǎng)牌榜的首位.運(yùn)動(dòng)會(huì)期間有甲、乙等五名志愿者被分配到射擊、田徑、籃球、游泳四個(gè)運(yùn)動(dòng)場(chǎng)地提供服務(wù),要求每個(gè)人都要被派出去提供服務(wù),且每個(gè)場(chǎng)地都要有志愿者服務(wù),則甲和乙恰好在同一組的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知在多面體![]() 中,平面
中,平面![]() 平面
平面![]() ,且四邊形
,且四邊形![]() 為正方形,且
為正方形,且![]() //
//![]() ,
,![]() ,
,![]() ,點(diǎn)
,點(diǎn)![]() ,
,![]() 分別是
分別是![]() ,
,![]() 的中點(diǎn).
的中點(diǎn).

(1)求證:![]() 平面
平面![]() ;
;
(2)求平面![]() 與平面
與平面![]() 所成的銳二面角的余弦值.
所成的銳二面角的余弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
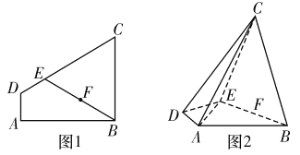
【題目】如圖1,四邊形![]() 為直角梯形,
為直角梯形,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 為線段
為線段![]() 上一點(diǎn),滿(mǎn)足
上一點(diǎn),滿(mǎn)足![]() ,
,![]() 為
為![]() 的中點(diǎn),現(xiàn)將梯形沿
的中點(diǎn),現(xiàn)將梯形沿![]() 折疊(如圖2),使平面
折疊(如圖2),使平面![]() 平面
平面![]() .
.
(1)求證:平面![]() 平面
平面![]() ;
;
(2)能否在線段![]() 上找到一點(diǎn)
上找到一點(diǎn)![]() (端點(diǎn)除外)使得直線
(端點(diǎn)除外)使得直線![]() 與平面
與平面![]() 所成角的正弦值為
所成角的正弦值為![]() ?若存在,試確定點(diǎn)
?若存在,試確定點(diǎn)![]() 的位置;若不存在,請(qǐng)說(shuō)明理由.
的位置;若不存在,請(qǐng)說(shuō)明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知正項(xiàng)等比數(shù)列{an}滿(mǎn)足a1=2,2a2=a4﹣a3,數(shù)列{bn}滿(mǎn)足bn=1+2log2an.
(1)求數(shù)列{an},{bn}的通項(xiàng)公式;
(2)令cn=anbn,求數(shù)列{cn}的前n項(xiàng)和Sn;
(3)若λ>0,且對(duì)所有的正整數(shù)n都有2λ2﹣kλ+2![]() 成立,求k的取值范圍.
成立,求k的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖所示的幾何體B-ACDE中,AB⊥AC,AB=4,AC=3,DC⊥平面ABC,EA⊥平面ABC,點(diǎn)M在線段BC上,且AM=![]() .
.
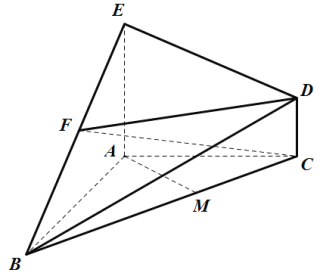
(1)證明:AM⊥平面BCD;
(2)若點(diǎn)F為線段BE的中點(diǎn),且三棱錐F-BCD的體積為1,求CD的長(zhǎng)度.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知數(shù)列![]() 的各項(xiàng)均為正數(shù),記數(shù)列
的各項(xiàng)均為正數(shù),記數(shù)列![]() 的前n項(xiàng)和為
的前n項(xiàng)和為![]() ,數(shù)列
,數(shù)列![]() 的前n項(xiàng)和為
的前n項(xiàng)和為![]() ,且
,且![]() .
.
(1)求![]() 的值;
的值;
(2)求數(shù)列![]() 的通項(xiàng)公式;
的通項(xiàng)公式;
(3)若![]() ,且
,且![]() 成等比數(shù)列,求k和t的值.
成等比數(shù)列,求k和t的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】在直角坐標(biāo)系![]() 中,直線
中,直線![]() 的參數(shù)方程為
的參數(shù)方程為![]() (
(![]() 為參數(shù),
為參數(shù),![]() 為直線
為直線![]() 的傾斜角),以坐標(biāo)原點(diǎn)
的傾斜角),以坐標(biāo)原點(diǎn)![]() 為極點(diǎn),以
為極點(diǎn),以![]() 軸正半軸為極軸,建立極坐標(biāo)系,曲線
軸正半軸為極軸,建立極坐標(biāo)系,曲線![]() 的極坐標(biāo)方程為
的極坐標(biāo)方程為![]() .
.
(1)寫(xiě)出曲線![]() 的直角坐標(biāo)方程,并求
的直角坐標(biāo)方程,并求![]() 時(shí)直線
時(shí)直線![]() 的普通方程;
的普通方程;
(2)直線![]() 和曲線
和曲線![]() 交于
交于![]() 、
、![]() 兩點(diǎn),點(diǎn)
兩點(diǎn),點(diǎn)![]() 的直角坐標(biāo)為
的直角坐標(biāo)為![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】函數(shù)f(x)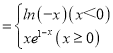 ,若關(guān)于x的方程f2(x)﹣af(x)+a﹣a2=0有四個(gè)不等的實(shí)數(shù)根,則a的取值范圍是( )
,若關(guān)于x的方程f2(x)﹣af(x)+a﹣a2=0有四個(gè)不等的實(shí)數(shù)根,則a的取值范圍是( )
A.![]() B.(﹣∞,﹣1)∪[1,+∞)
B.(﹣∞,﹣1)∪[1,+∞)
C.(﹣∞,﹣1)∪{1}D.(﹣1,0)∪{1}
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com