
【題目】垃圾分類,是指按一定規定或標準將垃圾分類儲存、分類投放和分類搬運,從而轉變成公共資源的一系列活動的總稱.分類的目的是提高垃圾的資源價值和經濟價值,力爭物盡其用.2019年6月25日,生活垃圾分類制度入法.到2020年底,先行先試的46個重點城市,要基本建成垃圾分類處理系統;其他地級城市實現公共機構生活垃圾分類全覆蓋.某機構欲組建一個有關“垃圾分類”相關事宜的項目組,對各個地區“垃圾分類”的處理模式進行相關報道.該機構從600名員工中進行篩選,篩選方法:每位員工測試![]() ,
,![]() ,
,![]() 三項工作,3項測試中至少2項測試“不合格”的員工,將被認定為“暫定”,有且只有一項測試“不合格”的員工將再測試
三項工作,3項測試中至少2項測試“不合格”的員工,將被認定為“暫定”,有且只有一項測試“不合格”的員工將再測試![]() ,
,![]() 兩項,如果這兩項中有1項以上(含1項)測試“不合格”,將也被認定為“暫定”,每位員工測試
兩項,如果這兩項中有1項以上(含1項)測試“不合格”,將也被認定為“暫定”,每位員工測試![]() ,
,![]() ,
,![]() 三項工作相互獨立,每一項測試“不合格”的概率均為
三項工作相互獨立,每一項測試“不合格”的概率均為![]() .
.
(1)記某位員工被認定為“暫定”的概率為![]() ,求
,求![]() ;
;
(2)每位員工不需要重新測試的費用為90元,需要重新測試的總費用為150元,除測試費用外,其他費用總計為1萬元,若該機構的預算為8萬元,且該600名員工全部參與測試,問上述方案是否會超過預算?請說明理由.
【答案】(1)![]() ;(2)不會超過預算.
;(2)不會超過預算.
【解析】
(1)利用互斥事件的概率加法計算公式和n次獨立重復實驗的概率計算公式進行求解即可;
(2)設每位員工測試的費用為![]() 元,則
元,則![]() 可能的取值為
可能的取值為![]() ,利用n次獨立重復實驗的概率計算公式和離散型隨機變量的數學期望公式求出數學期望的表達式,通過構造函數,利用導數判斷函數的單調性求最值即可.
,利用n次獨立重復實驗的概率計算公式和離散型隨機變量的數學期望公式求出數學期望的表達式,通過構造函數,利用導數判斷函數的單調性求最值即可.
(1)由題意知,每位員工首輪測試被認定為“暫定”的概率為![]() ,
,
每位員工再次測試被認定為“暫定”的概率為![]() ,
,
綜上可知,每位員工被認定為“暫定”的概率為
![]()
![]()
![]() +
+![]()
![]() ,
,
(2)設每位員工測試的費用為![]() 元,則
元,則![]() 可能的取值為
可能的取值為![]() ,
,
由題意知,![]() ,
,![]() ,
,
所以隨機變量![]() 的數學期望為
的數學期望為
![]() (元),
(元),![]() ,
,
令![]() ,則
,則
![]() ,
,
所以當![]() 時,
時,![]() ;當
;當![]() 時,
時,![]() ;
;
所以函數![]() 在
在![]() 上單調遞增,在
上單調遞增,在![]() 上單調遞減,
上單調遞減,
所以![]() ,即
,即![]() (元),
(元),
所以此方案的最高費用為![]() (萬元),
(萬元),
綜上可知,若以此方案實施不會超過預算.


 尖子生新課堂課時作業系列答案
尖子生新課堂課時作業系列答案 英才計劃同步課時高效訓練系列答案
英才計劃同步課時高效訓練系列答案科目:高中數學 來源: 題型:
【題目】2019年是中華人民共和國成立70周年.為了讓人民了解建國70周年的風雨歷程,某地的民調機構隨機選取了該地的100名市民進行調查,將他們的年齡分成6段:![]() ,
,![]() ,…,
,…,![]() ,并繪制了如圖所示的頻率分布直方圖.
,并繪制了如圖所示的頻率分布直方圖.

(1)現從年齡在![]() ,
,![]() ,
,![]() 內的人員中按分層抽樣的方法抽取8人,再從這8人中隨機選取3人進行座談,用
內的人員中按分層抽樣的方法抽取8人,再從這8人中隨機選取3人進行座談,用![]() 表示年齡在
表示年齡在![]() )內的人數,求
)內的人數,求![]() 的分布列和數學期望;
的分布列和數學期望;
(2)若用樣本的頻率代替概率,用隨機抽樣的方法從該地抽取20名市民進行調查,其中有![]() 名市民的年齡在
名市民的年齡在![]() 的概率為
的概率為![]() .當
.當![]() 最大時,求
最大時,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() (其中
(其中![]() 是常數,且
是常數,且![]() ),曲線
),曲線![]() 在
在![]() 處的切線方程為
處的切線方程為![]() .
.
(1)求![]() 的值;
的值;
(2)若存在![]() (其中
(其中![]() 是自然對數的底),使得
是自然對數的底),使得![]() 成立,求
成立,求![]() 的取值范圍;
的取值范圍;
(3)設![]() ,若對任意
,若對任意![]() ,均存在
,均存在![]() ,使得方程
,使得方程![]() 有三個不同的實數解,求實數
有三個不同的實數解,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某單位N名員工參加“社區低碳你我他”活動.他們的年齡在25歲至50歲之間.按年齡分組:第1組[25,30),第2組[30,35),第3組[35,40),第4組[40,45),第5組[45,50],得到的頻率分布直方圖如圖所示.下表是年齡的頻率分布表.

區間 | [25,30) | [30,35) | [35,40) | [40,45) | [45,50] |
人數 | 25 | a | b | ||
(1)求正整數a,b,N的值;
(2)現要從年齡較小的第1,2,3組中用分層抽樣的方法抽取6人,則年齡在第1,2,3組的人數分別是
多少?
(3)在(2)的條件下,從這6人中隨機抽取2人參加社區宣傳交流活動,求恰有1人在第3組的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】七巧板是一種古老的中國傳統智力玩具,是由七塊板組成.而這七塊板可拼成許多圖形,人物、動物、建筑物等,在18世紀,七巧板流傳到了國外,至今英國劍橋大學的圖書館里還珍藏著一部《七巧圖譜》.若用七巧板(圖1為正方形),拼成一只雄雞(圖2),在雄雞平面圖形上隨機取一點,則恰好取自雄雞雞頭或雞尾(陰影部分)的概率為( )
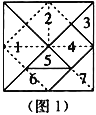
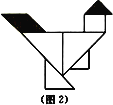
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的兩個焦點
的兩個焦點![]() ,動點
,動點![]() 在橢圓上,且使得
在橢圓上,且使得![]() 的點
的點![]() 恰有兩個,動點
恰有兩個,動點![]() 到焦點
到焦點![]() 的距離的最大值為
的距離的最大值為![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)如圖,以橢圓![]() 的長軸為直徑作圓
的長軸為直徑作圓![]() ,過直線
,過直線![]() 上的動點
上的動點![]() 作圓
作圓![]() 的兩條切線,設切點分別為
的兩條切線,設切點分別為![]() ,若直線
,若直線![]() 與橢圓
與橢圓![]() 交于不同的兩點
交于不同的兩點![]() ,求
,求![]() 的取值范圍.
的取值范圍.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在三棱錐D-ABC中,![]() ,且
,且![]() ,
,![]() ,M,N分別是棱BC,CD的中點,下面結論正確的是( )
,M,N分別是棱BC,CD的中點,下面結論正確的是( )
A.![]() B.
B.![]() 平面ABD
平面ABD
C.三棱錐A-CMN的體積的最大值為![]() D.AD與BC一定不垂直
D.AD與BC一定不垂直
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com