
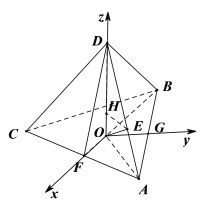
【題目】如圖,已知四面體![]() 中,
中,![]() ,且
,且![]() 兩兩互相垂直,點
兩兩互相垂直,點![]() 是
是![]() 的中心.
的中心.

(1)求二面角![]() 的大小(用反三角函數表示);
的大小(用反三角函數表示);
(2)過![]() 作
作![]() ,垂足為
,垂足為![]() ,求
,求![]() 繞直線
繞直線![]() 旋轉一周所形成的幾何體的體積;
旋轉一周所形成的幾何體的體積;
(3)將![]() 繞直線
繞直線![]() 旋轉一周,則在旋轉過程中,直線
旋轉一周,則在旋轉過程中,直線![]() 與直線
與直線![]() 所成角記為
所成角記為![]() ,求
,求![]() 的取值范圍.
的取值范圍.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)根據三垂線定理,取![]() 中點
中點![]() ,連接
,連接![]() 和
和![]() ,所以
,所以![]() ,則
,則![]() 即為二面角
即為二面角![]() 的平面角,解三角形即可求出二面角
的平面角,解三角形即可求出二面角![]() 的大小;
的大小;
(2)按照圓錐的定義可知,![]() 繞直線
繞直線![]() 旋轉一周所形成的幾何體為兩個圓錐的組合體,計算出圓錐底面半徑以及圓錐的高,即可求出體積;
旋轉一周所形成的幾何體為兩個圓錐的組合體,計算出圓錐底面半徑以及圓錐的高,即可求出體積;
(3)取![]() 中點
中點![]() ,連接
,連接![]() ,以
,以![]() 為坐標原點,
為坐標原點,![]() 為
為![]() 軸,
軸,![]() 為
為![]() 軸,
軸,![]() 為
為![]() 軸,建立空間直角坐標系,設出A點坐標,求出
軸,建立空間直角坐標系,設出A點坐標,求出![]() 和
和![]() ,利用向量的夾角公式可求出
,利用向量的夾角公式可求出![]() ,最后根據平面幾何知識即可求出
,最后根據平面幾何知識即可求出![]() 的取值范圍.
的取值范圍.
(1)取![]() 中點
中點![]() ,連接
,連接![]() 和
和![]() ,因為點
,因為點![]() 在平面
在平面![]() 的射影
的射影![]() 在中線
在中線![]() 上,
上,
所以![]() ,由二面角的定義可知,
,由二面角的定義可知,![]() 即為二面角
即為二面角![]() 的平面角.在
的平面角.在![]() 中,
中,![]() ,
,![]() ,
,
所以![]() ,即
,即![]() ,
,
所以二面角![]() 的大小為
的大小為![]() .
.
(2)過![]() 作
作![]() ,經計算得
,經計算得![]() ,
,
由此得![]() ,
,
所以![]() 繞直線
繞直線![]() 旋轉一周所形成的幾何體的體積:
旋轉一周所形成的幾何體的體積:
![]() .
.
(3)取![]() 中點
中點![]() ,連接
,連接![]() ,以
,以![]() 為坐標原點,
為坐標原點,![]() 為
為![]() 軸,
軸,![]() 為
為![]() 軸,
軸,![]() 為
為![]() 軸,建立空間直角坐標系,
軸,建立空間直角坐標系,
則![]() ,
,![]() ,
,![]() ,
,
設![]() ,則
,則![]() ,
,![]() ,
,
所以![]() ,
,
在![]() 平面上,點
平面上,點![]() 的軌跡方程為
的軌跡方程為![]() ,
,
令![]() ,則
,則![]() ,
,
所以![]() ,
,
于是![]() .
.


 舉一反三期末百分沖刺卷系列答案
舉一反三期末百分沖刺卷系列答案科目:高中數學 來源: 題型:
【題目】近年來,來自“一帶一路”沿線的20國青年評選出了中國的“新四大發明”:高鐵、掃碼支付、共享單車和網購.其中共享單車既響應綠色出行號召,節能減排,保護環境,又方便人們短距離出行,增強靈活性.某城市試投放3個品牌的共享單車分別為紅車、黃車、藍車,三種車的計費標準均為每15分鐘(不足15分鐘按15分鐘計)1元,按每日累計時長結算費用,例如某人某日共使用了24分鐘,系統計時為30分鐘.A同學統計了他1個月(按30天計)每天使用共享單車的時長如莖葉圖所示,不考慮每月自然因素和社會因素的影響,用頻率近似代替概率.設A同學每天消費![]() 元.
元.
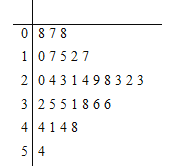
(1)求![]() 的分布列及數學期望;
的分布列及數學期望;
(2)各品牌為推廣用戶使用,推出APP注冊會員的優惠活動:紅車月功能使用費8元,每天消費打5折;黃車月功能使用費20元,每天前15分鐘免費,之后消費打8折;藍車月功能使用費45元,每月使用22小時之內免費,超出部分按每15分鐘1元計費.設![]() 分別為紅車,黃車,藍車的月消費,寫出
分別為紅車,黃車,藍車的月消費,寫出![]() 與
與![]() 的函數關系式,參考(1)的結果,A同學下個月選擇其中一個注冊會員,他選哪個費用最低?
的函數關系式,參考(1)的結果,A同學下個月選擇其中一個注冊會員,他選哪個費用最低?
(3)該城市計劃3個品牌的共享單車共3000輛正式投入使用,為節約居民開支,隨機調查了100名用戶一周的平均使用時長如下表:
時長 | (0,15] | (15,30] | (30,45] | (45,60] |
人數 | 16 | 45 | 34 | 5 |
在(2)的活動條件下,每個品牌各應該投放多少輛?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(1)集合![]() ,
,![]() 或
或![]() ,對于任意
,對于任意![]() ,定義
,定義![]() ,對任意
,對任意![]() ,定義
,定義![]() ,記
,記![]() 為集合
為集合![]() 的元素個數,求
的元素個數,求![]() 的值;
的值;
(2)在等差數列![]() 和等比數列
和等比數列![]() 中,
中,![]() ,
,![]() ,是否存在正整數
,是否存在正整數![]() ,使得數列
,使得數列![]() 的所有項都在數列
的所有項都在數列![]() 中,若存在,求出所有的
中,若存在,求出所有的![]() ,若不存在,說明理由;
,若不存在,說明理由;
(3)已知當![]() 時,有
時,有![]() ,根據此信息,若對任意
,根據此信息,若對任意![]() ,都有
,都有![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,設直線
,設直線![]() 分別是曲線
分別是曲線![]() 的兩條不同的切線;
的兩條不同的切線;
(1)若函數![]() 為奇函數,且當
為奇函數,且當![]() 時,
時,![]() 有極小值為-4;
有極小值為-4;
(i)求![]() 的值;
的值;
(ii)若直線![]() 亦與曲線
亦與曲線![]() 相切,且三條不同的直線
相切,且三條不同的直線![]() 交于點
交于點![]() ,求實數m的取值范圍;
,求實數m的取值范圍;
(2)若直線![]() ,直線
,直線![]() 與曲線
與曲線![]() 切于點B且交曲線
切于點B且交曲線![]() 于點D,直線
于點D,直線![]() 與曲線
與曲線![]() 切于點C且交曲線
切于點C且交曲線![]() 于點A,記點
于點A,記點![]() 的橫坐標分別為
的橫坐標分別為![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,M為△ABC的中線AD的中點,過點M的直線分別交線段AB、AC于點P、Q兩點,設![]() ,
,![]() ,記
,記![]() .
.
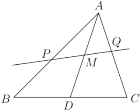
(1)求![]() 的值;
的值;
(2)求函數![]() 的解析式(指明定義域);
的解析式(指明定義域);
(3)設![]() ,
,![]() ,若對任意
,若對任意![]() ,總存在
,總存在![]() ,使得
,使得![]() 成立,求實數a的取值范圍.
成立,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點![]() 是函數
是函數![]() 的圖象上的一點,等比數列
的圖象上的一點,等比數列![]() 的前
的前![]() 項和為
項和為![]() ,數列
,數列![]()
![]() 的首項為
的首項為![]() ,且前
,且前![]() 項和
項和![]() 滿足:
滿足:![]() .
.
(1)求數列![]() ,
,![]() 的通項公式;
的通項公式;
(2)若數列![]() 的通項
的通項 ,求數列
,求數列![]() 的前
的前![]() 項和
項和![]() ;
;
(3)若數列 的前項和為
的前項和為![]() ,是否存在最大的整數
,是否存在最大的整數![]() ,使得對任意的正整數n,均有
,使得對任意的正整數n,均有![]() 總成立?若成立,求出t;若不存在,請說明理由.
總成立?若成立,求出t;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設拋物線C的頂點在原點,焦點F在y軸上,開口向上,焦點到準線的距離為![]()
(1)求拋物線的標準方程;
(2)已知拋物線C過焦點F的動直線l交拋物線于A、B兩點,O為坐標原點,求證: ![]() 為定值.
為定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某網站用“100分制”調查一社區人們的幸福度.現從調查人群中隨機抽取10名,以下莖葉圖記錄了他們的幸福度分數(以十位數字為莖,個位數字為葉);若幸福度不低于95分,則稱該人的幸福度為“極幸福”.

(1)從這10人中隨機選取3人,記![]() 表示抽到“極幸福”的人數,求
表示抽到“極幸福”的人數,求![]() 的分布列及數學期望;
的分布列及數學期望;
(2)以這10人的樣本數據來估計整個社區的總體數據,若從該社區(人數很多)任選3人,記![]() 表示抽到“極幸福”的人數,求
表示抽到“極幸福”的人數,求![]() 的數學期望和方差.
的數學期望和方差.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐P-ABCD中,底面ABCD為正方形,平面PAD⊥平面ABCD,點M在線段PPD//平面MAC,PA=PD=![]() ,AB=4.
,AB=4.
(I)求證:M為PB的中點;
(II)求二面角B-PD-A的大小;
(III)求直線MC與平面BDP所成角的正弦值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com