【題目】已知拋物線
的焦點為
，準(zhǔn)線為
，拋物線
上存在一點
，過點作
，垂足為
，使
是等邊三角形且面積為
.
（1）求拋物線的方程；
（2）若點
是圓
與拋物線的一個交點，點
，當(dāng)
取得最小值時，求此時圓
的方程.
【答案】（1）
（2）
【解析】
（1）利用等邊三角形可得
值，從而得到拋物線
的方程；
（2）設(shè)
的坐標(biāo)為
，易得
，所以
，結(jié)合最值即可得到圓
的方程.
解：（1）如圖所示，
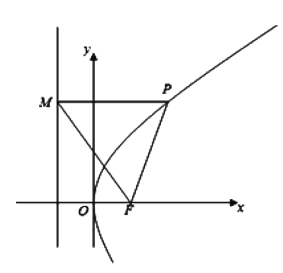
∵等邊
的面積為
，
設(shè)邊長為
，
∴
，∴
，∴
∵
，∴
所以拋物線的方程是.
（2）法一：設(shè)的坐標(biāo)為，因為拋物線：的焦點
，
，
，
所以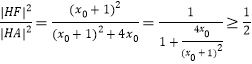
當(dāng)且僅當(dāng)
時取等號，即當(dāng)
取最小值時，點坐標(biāo)為
把點坐標(biāo)代入圓的方程可得.
法二：設(shè)的坐標(biāo)為
，因為拋物線：的焦點，
，
，
所以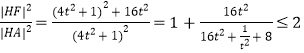
，當(dāng)且僅當(dāng)
時取等號，
即當(dāng)取最小值時，點坐標(biāo)為
把點坐標(biāo)代入圓的方程可得.
閱讀快車系列答案科目：高中數(shù)學(xué) 來源： 題型：
【題目】在2018年俄羅斯世界杯期間,莫斯科的部分餐廳經(jīng)營了來自中國的小龍蝦,這些小龍蝦標(biāo)有等級代碼.為得到小龍蝦等級代碼數(shù)值
與銷售單價
之間的關(guān)系,經(jīng)統(tǒng)計得到如下數(shù)據(jù)：
等級代碼數(shù)值 | 38 | 48 | 58 | 68 | 78 | 88 |
銷售單價 | 16.8 | 18.8 | 20.8 | 22.8 | 24 | 25.8 |
（1）已知銷售單價與等級代碼數(shù)值之間存在線性相關(guān)關(guān)系,求關(guān)于的線性回歸方程(系數(shù)精確到0.1)；
（2）若莫斯科某餐廳銷售的中國小龍蝦的等級代碼數(shù)值為98，請估計該等級的中國小龍蝦銷售單價為多少元？
參考公式：對一組數(shù)據(jù)
,
，····
,其回歸直線
的斜率和截距最小二乘估計分別為：
,
.
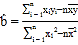參考數(shù)據(jù)：
,
.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】某種植物感染
病毒極易導(dǎo)致死亡，某生物研究所為此推出了一種抗病毒的制劑，現(xiàn)對20株感染了病毒的該植株樣本進(jìn)行噴霧試驗測試藥效.測試結(jié)果分“植株死亡”和“植株存活”兩個結(jié)果進(jìn)行統(tǒng)計；并對植株吸收制劑的量(單位：mg)進(jìn)行統(tǒng)計.規(guī)定：植株吸收在6mg（包括6mg）以上為“足量”，否則為“不足量”.現(xiàn)對該20株植株樣本進(jìn)行統(tǒng)計，其中 “植株存活”的13株，對制劑吸收量統(tǒng)計得下表.已知“植株存活”但“制劑吸收不足量”的植株共1株.
編號 | 01 | 02 | 03 | 04 | 05 | 06 | 07 | 08 | 09 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
吸收量(mg) | 6 | 8 | 3 | 8 | 9 | 5 | 6 | 6 | 2 | 7 | 7 | 5 | 10 | 6 | 7 | 8 | 8 | 4 | 6 | 9 |
（1）完成以下
列聯(lián)表，并判斷是否可以在犯錯誤概率不超過1%的前提下，認(rèn)為“植株的存活”與“制劑吸收足量”有關(guān)？
吸收足量 | 吸收不足量 | 合計 | |
植株存活 | 1 | ||
植株死亡 | |||
合計 | 20 |
（2）①若在該樣本“吸收不足量”的植株中隨機(jī)抽取3株，記
為“植株死亡”的數(shù)量，求得分布列和期望
；
②將頻率視為概率，現(xiàn)在對已知某塊種植了1000株并感染了病毒的該植物試驗田里進(jìn)行該藥品噴霧試驗，設(shè)“植株存活”且“吸收足量”的數(shù)量為隨機(jī)變量
，求
.
參考數(shù)據(jù)：
，其中
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知橢圓C：
（
）的兩焦點與短軸的一個端點的連線構(gòu)成等腰直角三角形，直線
與以橢圓C的右焦點為圓心，以橢圓的半長軸長為半徑的圓相切．
（1）求橢圓C的方程；
（2）設(shè)P為橢圓C上一點，若過點
的直線l與橢圓C相交于不同的兩點S和T，滿足
（O為坐標(biāo)原點），求實數(shù)t的取值范圍．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】下列說法：
①對于獨立性檢驗，
的值越大，說明兩事件相關(guān)程度越大；
②以模型
去擬合一組數(shù)據(jù)時，為了求出回歸方程，設(shè)
，將其變換后得到線性方程
，則
，
的值分別是
和0.3；
③已知隨機(jī)變量
，若
，則
（
）的值為
；
④通過回歸直線
及回歸系數(shù)
，可以精確反映變量的取值和變化趨勢．
其中錯誤的選項是（ ）
A.①B.②C.③D.④
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】“過大年，吃水餃”是我國不少地方過春節(jié)的一大習(xí)俗，2020年春節(jié)前夕，A市某質(zhì)檢部門隨機(jī)抽取了100包某種品牌的速凍水餃，檢測其某項質(zhì)量指標(biāo)．
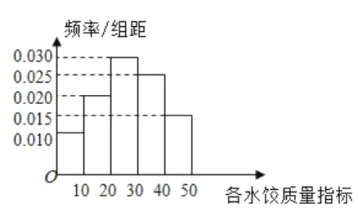
（1）求所抽取的100包速凍水餃該項質(zhì)量指標(biāo)值的樣本平均數(shù)
（同一組中的數(shù)據(jù)用該組區(qū)間的中點值作代表）；
（2）①由直方圖可以認(rèn)為，速凍水餃的該項質(zhì)量指標(biāo)值
服從正態(tài)分布
，利用該正態(tài)分布，求落在
內(nèi)的概率；
②將頻率視為概率，若某人從某超市購買了4包這種品牌的速凍水餃，記這4包速凍水餃中這種質(zhì)量指標(biāo)值位于
內(nèi)的包數(shù)為
，求的分布列和數(shù)學(xué)期望．
附：①計算得所抽查的這100包速凍水餃的質(zhì)量指標(biāo)的標(biāo)準(zhǔn)差為
；
②若
，則
，
．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】關(guān)于函數(shù)
有下述四個結(jié)論：
①函數(shù)
的圖象把圓
的面積兩等分
②是周期為
的函數(shù)
③函數(shù)在區(qū)間
上有
個零點
④函數(shù)在區(qū)間上單調(diào)遞減
其中所有不正確結(jié)論的編號是（ ）
A.①③④B.②③C.①④D.①③
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知函數(shù)
.
（1）若函數(shù)
在
時取得極值，求實數(shù)
的值；
（2）若
對任意
恒成立，求實數(shù)的取值范圍.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知集合A＝{x|y＝ln（﹣x2﹣x+12）}，B＝{x|m﹣1＜x＜2m+1，m∈R}．
（1）若m＝2，求（RA）∩B；
（2）若A∩B＝B，求實數(shù)m的取值范圍．
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
