
【題目】移動支付(支付寶及微信支付)已經漸漸成為人們購物消費的一種支付方式,為調查市民使用移動支付的年齡結構,隨機對100位市民做問卷調查得到![]() 列聯表如下:
列聯表如下:
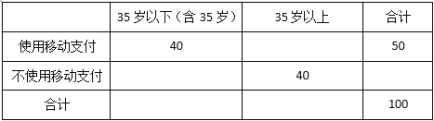
(1)將上![]() 列聯表補充完整,并請說明在犯錯誤的概率不超過0.10的前提下,認為支付方式與年齡是否有關?
列聯表補充完整,并請說明在犯錯誤的概率不超過0.10的前提下,認為支付方式與年齡是否有關?
(2)在使用移動支付的人群中采用分層抽樣的方式抽取10人做進一步的問卷調查,從這10人隨機中選出3人頒發參與獎勵,設年齡都低于35歲(含35歲)的人數為![]() ,求
,求![]() 的分布列及期望.
的分布列及期望.

(參考公式: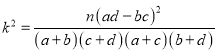 (其中
(其中![]() )
)
【答案】(1)列聯表見解析,在犯錯誤的概率不超過0.10的前提下,認為支付方式與年齡有關;(2)分布列見解析,期望為![]() .
.
【解析】
(1)根據題中所給的條件補全列聯表,根據列聯表求出觀測值,把觀測值同臨界值進行比較,得到能在犯錯誤的概率不超過0.10的前提下,認為支付方式與年齡有關.
(2)首先確定![]() 的取值,求出相應的概率,可得分布列和數學期望.
的取值,求出相應的概率,可得分布列和數學期望.
(1)根據題意及![]() 列聯表可得完整的
列聯表可得完整的![]() 列聯表如下:
列聯表如下:
35歲以下(含35歲) | 35歲以上 | 合計 | |
使用移動支付 | 40 | 10 | 50 |
不使用移動支付 | 10 | 40 | 50 |
合計 | 50 | 50 | 100 |
根據公式可得![]() ,
,
所以在犯錯誤的概率不超過0.10的前提下,認為支付方式與年齡有關.
(2)根據分層抽樣,可知35歲以下(含35歲)的人數為8人,35歲以上的有2人,
所以獲得獎勵的35歲以下(含35歲)的人數為![]() ,
,
則![]() 的可能為1,2,3,且
的可能為1,2,3,且
![]() ,
,![]() ,
,![]() ,
,
其分布列為
| 1 | 2 | 3 |
|
|
|
|
![]() .
.


科目:高中數學 來源: 題型:
【題目】某學生社團對![]() 年元宵節當天游覽磁器口古鎮景區的游客滿意度抽樣調查,從當日
年元宵節當天游覽磁器口古鎮景區的游客滿意度抽樣調查,從當日![]() 萬名游客中隨機抽取
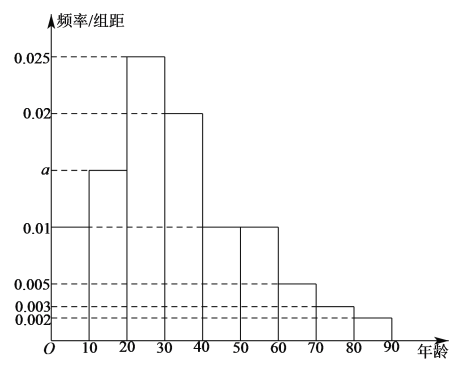
萬名游客中隨機抽取![]() 人進行統計,結果如下圖的頻率分布表和頻率分布直方圖:
人進行統計,結果如下圖的頻率分布表和頻率分布直方圖:
年齡 | 頻數 | 頻率 | 滿意 | 不滿意 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
合計 |
|
|
|
|
(1)求![]() 、
、![]() 、
、![]() 的值;
的值;
(2)利用頻率分布直方圖,估算游客的平均年齡和年齡的中位數;
(3)稱年齡不低于![]() 歲的人群為“安逸人群”,完成
歲的人群為“安逸人群”,完成![]() 列聯表,并判斷是否有
列聯表,并判斷是否有![]() 的把握認為游客的滿意度與“安逸人群”人數相關.
的把握認為游客的滿意度與“安逸人群”人數相關.
|
| 合計 | |
滿意 | |||
不滿意 | |||
合計 |
參考公式: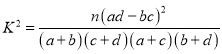 ,其中
,其中![]() .
.
參考數據:![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,直線l的參數方程為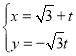 (t為參數),以坐標原點為極點,x軸正半軸為極軸,建立極坐標系,已知曲線C的極坐標方程為
(t為參數),以坐標原點為極點,x軸正半軸為極軸,建立極坐標系,已知曲線C的極坐標方程為![]() .
.
(1)求直線l的普通方程與曲線C的直角坐標方程;
(2)設點![]() ,直線l與曲線C交于不同的兩點A、B,求
,直線l與曲線C交于不同的兩點A、B,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設曲線![]() 上一點
上一點![]() 到焦點的距離為3.
到焦點的距離為3.
(1)求曲線C方程;
(2)設P,Q為曲線C上不同于原點O的任意兩點,且滿足以線段PQ為直徑的圓過原點O,試問直線PQ是否恒過定點?若恒過定點,求出定點坐標;若不恒過定點,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓C:![]() (
(![]() )的兩焦點與短軸兩端點圍成面積為12的正方形.
)的兩焦點與短軸兩端點圍成面積為12的正方形.
(1)求橢圓C的標準方程;
(2)我們稱圓心在橢圓上運動,半徑為![]() 的圓是橢圓的“衛星圓”.過原點O作橢圓C的“衛星圓”的兩條切線,分別交橢圓C于A、B兩點,若直線
的圓是橢圓的“衛星圓”.過原點O作橢圓C的“衛星圓”的兩條切線,分別交橢圓C于A、B兩點,若直線![]() 、
、![]() 的斜率為
的斜率為![]() 、
、![]() ,當
,當![]() 時,求此時“衛星圓”的個數.
時,求此時“衛星圓”的個數.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com