
【題目】目前,青蒿素作為一線抗瘧藥品得到大力推廣某農科所為了深入研究海拔因素對青蒿素產量的影響,在山上和山下的試驗田中分別種植了![]() 株青蒿進行對比試驗.現在從山上和山下的試驗田中各隨機選取了
株青蒿進行對比試驗.現在從山上和山下的試驗田中各隨機選取了![]() 株青蒿作為樣本,每株提取的青蒿素產量(單位:克)如下表所示:
株青蒿作為樣本,每株提取的青蒿素產量(單位:克)如下表所示:
編號位置 | ① | ② | ③ | ④ |
山上 |
|
|
|
|
山下 |
|
|
|
|
(1)根據樣本數據,試估計山下試驗田青蒿素的總產量;
(2)記山上與山下兩塊試驗田單株青蒿素產量的方差分別為![]() ,
,![]() ,根據樣本數據,試估計
,根據樣本數據,試估計![]() 與
與![]() 的大小關系(只需寫出結論);
的大小關系(只需寫出結論);
(3)從樣本中的山上與山下青蒿中各隨機選取![]() 株,記這
株,記這![]() 株的產量總和為
株的產量總和為![]() 的概率.
的概率.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)由山下試驗田![]() 株青蒿樣本青蒿素產量數據,能求出樣本平均數和山下試驗田
株青蒿樣本青蒿素產量數據,能求出樣本平均數和山下試驗田![]() 株青蒿的青蒿素產量
株青蒿的青蒿素產量![]() 的估計值;
的估計值;
(2)比較山上、山下單株青蒿樣本青蒿素產量數據的離散程度,可得出![]() 、
、![]() 的大小關系;
的大小關系;
(3)記事件![]() ,列出表格得出從山上與山下青蒿中各隨機選取
,列出表格得出從山上與山下青蒿中各隨機選取![]() 株的青蒿素產量總和,從表格中得出基本事件的總數,并得出事件
株的青蒿素產量總和,從表格中得出基本事件的總數,并得出事件![]() 所包含的基本事件數,利用古典概型的概率公式可計算出事件
所包含的基本事件數,利用古典概型的概率公式可計算出事件![]() 的概率.
的概率.
(1)由山下試驗田![]() 株青蒿樣本青蒿素產量數據,得樣本平均數
株青蒿樣本青蒿素產量數據,得樣本平均數![]() ,
,
則山下試驗田![]() 株青蒿的青蒿素的總產量
株青蒿的青蒿素的總產量![]() 估算為:
估算為:![]() ;
;
(2)由樣本中山上、山下單株青蒿素產量的離散程度知![]() ;
;
(3)記![]() 為事件
為事件![]() ,列表:
,列表:
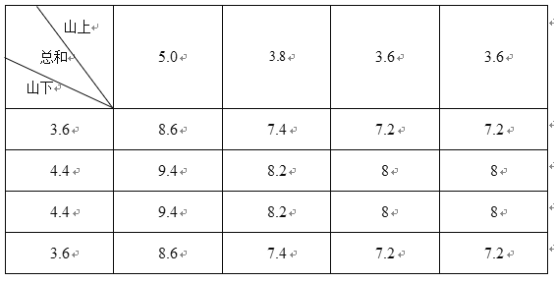
由上表可以看出,這![]() 株的產量總和
株的產量總和![]() 的所有情況共有
的所有情況共有![]() 種,
種,
而其中![]() 的情況共有
的情況共有![]() 種,故:
種,故:![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】(2017高考新課標Ⅲ,理19)如圖,四面體ABCD中,△ABC是正三角形,△ACD是直角三角形,∠ABD=∠CBD,AB=BD.
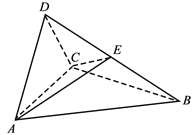
(1)證明:平面ACD⊥平面ABC;
(2)過AC的平面交BD于點E,若平面AEC把四面體ABCD分成體積相等的兩部分,求二面角D–AE–C的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】《山東省高考改革試點方案》規定:從2017年秋季高中入學的新生開始,不分文理科;2020年開始,高考總成績由語數外3門統考科目和物理、化學等六門選考科目構成.將每門選考科目的考生原始成績從高到低劃分為A、B+、B、C+、C、D+、D、E共8個等級.參照正態分布原則,確定各等級人數所占比例分別為3%、7%、16%、24%、24%、16%、7%、3%.選考科目成績計入考生總成績時,將A至E等級內的考生原始成績,依照等比例轉換法則,分別轉換到[91,100]、[81,90]、[71,80]、[61,70]、[51,60]、[41,50]、[31,40]、[21,30]八個分數區間,得到考生的等級成績.
某校高一年級共2000人,為給高一學生合理選科提供依據,對六個選考科目進行測試,其中物理考試原始成績基本服從正態分布N(60,169).
(Ⅰ)求物理原始成績在區間(47,86)的人數;
(Ⅱ)按高考改革方案,若從全省考生中隨機抽取3人,記X表示這3人中等級成績在區間[61,80]的人數,求X的分布列和數學期望.
(附:若隨機變量![]() ,則
,則![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某文體局為了解“跑團”每月跑步的平均里程,收集并整理了2018年1月至2018年11月期間“跑團”每月跑步的平均里程(單位:公里)的數據,繪制了下面的折線圖.根據折線圖,下列結論正確的是( )

A. 月跑步平均里程的中位數為6月份對應的里程數
B. 月跑步平均里程逐月增加
C. 月跑步平均里程高峰期大致在8、9月
D. 1月至5月的月跑步平均里程相對于6月至11月,波動性更小,變化比較平穩
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“柯西不等式”是由數學家柯西在研究數學分析中的“流數”問題時得到的,但從歷史的角度講,該不等式應當稱為柯西﹣﹣布尼亞科夫斯基﹣﹣施瓦茨不等式,因為正是后兩位數學家彼此獨立地在積分學中推而廣之,才將這一不等式推廣到完善的地步,在高中數學選修教材4﹣5中給出了二維形式的柯西不等式:(a2+b2)(c2+d2)≥(ac+bd)2當且僅當ad=bc(即![]() )時等號成立.該不等式在數學中證明不等式和求函數最值等方面都有廣泛的應用.根據柯西不等式可知函數
)時等號成立.該不等式在數學中證明不等式和求函數最值等方面都有廣泛的應用.根據柯西不等式可知函數![]() 的最大值及取得最大值時x的值分別為( )
的最大值及取得最大值時x的值分別為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】百鳥蛋,又稱九巧板,是類似于七巧板的益智拼圖.相傳是紀念哥倫布所制作的蛋形拼圖,故又有哥倫布蛋形拼圖一稱.如圖,九巧板由2個不規則四邊形、2個大三角形、1個小三角形、2個不規則三角形和兩個小扇形組成.在拼圖時必須使用所有組件,角與邊可相連接,但組件不能重疊.九巧板能拼擺出一百多種飛禽圖形,可說是變化無窮、極富趣味,因此也被稱為“百鳥朝鳳”拼板.已知拼圖中兩個大三角形(圖中陰影部分)為直角邊長為2的等腰直角三角形,現用隨機模擬的方法來估算此九巧板的總面積,隨機在九巧板內選取100個點,發現有34個點落在兩個大三角形內,則此九巧板的總面積約為______.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com