
【題目】設復平面上點Z1 , Z2 , …,Zn , …分別對應復數z1 , z2 , …,zn , …;
(1)設z=r(cosα+isinα),(r>0,α∈R),用數學歸納法證明:zn=rn(cosnα+isinnα),n∈Z+
(2)已知 ![]() ,且
,且 ![]() (cosα+isinα)(α為實常數),求出數列{zn}的通項公式;
(cosα+isinα)(α為實常數),求出數列{zn}的通項公式;
(3)在(2)的條件下,求 ![]() |+….
|+….
【答案】
(1)證明:當n=1時,左邊=r(cosθ+isinθ),右邊=r(cosθ+isinθ),
左邊=右邊,即n=1等式成立;
假設當n=k時等式成立,即:[r(cosθ+isinθ)]k=rk(coskθ+isinkθ),
則當n=k+1時,[r(cosθ+isinθ)]k+1=[r(cosθ+isinθ)]kr(cosθ+isinθ)
=rk(coskθ+isinkθ)rk(cosθ+isinθ)
=rk+1[(coskθcosθ﹣sinkθsinθ)+i(sinkθcosθ+coskθsinθ)]
=rk+1[cos(k+1)θ+isin(k+1)θ],
即當n=k+1時,等式成立;
綜上,對n∈N+,zn=rn(cosnα+isinnα)
(2)解: ![]() =
= ![]() =1,
=1,
且 ![]() (cosα+isinα)(α為實常數),
(cosα+isinα)(α為實常數),
∴數列{zn}是首項為Z1=1,公比為q= ![]() (cosα+isinα)的等比數列,
(cosα+isinα)的等比數列,
∴該數列的通項公式為Zn=Z1qn﹣1= ![]() [cos(n﹣1)α+isin(n﹣1)α]
[cos(n﹣1)α+isin(n﹣1)α]
(3)解:在(2)的條件下, ![]() =
= ![]() ﹣
﹣ ![]() =(
=( ![]() cosα﹣1,
cosα﹣1, ![]() sinα)
sinα)
∴| ![]() |=
|= ![]() .
.
![]() =
= ![]() [cosnα﹣2cos(n﹣1)α+i(sinnα﹣2sin(n﹣1)α)],
[cosnα﹣2cos(n﹣1)α+i(sinnα﹣2sin(n﹣1)α)],
![]() =
= ![]() =
= ![]() .
.
![]() |+…=
|+…= ![]() ×
× ![]() =
= ![]()
【解析】(1)按照數學歸納法的基本步驟即可證明等式成立;(2) ![]() =
=  =1,且
=1,且 ![]() (cosα+isinα)(α為實常數),可得數列{zn}是首項為Z1=1,公比為q=
(cosα+isinα)(α為實常數),可得數列{zn}是首項為Z1=1,公比為q= ![]() (cosα+isinα)的等比數列,利用等比數列的通項公式即可得出.(3)在(2)的條件下,
(cosα+isinα)的等比數列,利用等比數列的通項公式即可得出.(3)在(2)的條件下, ![]() =
= ![]() [cosnα﹣2cos(n﹣1)α+i(sinnα﹣2sin(n﹣1)α)],再利用數列極限求和公式即可得出.
[cosnα﹣2cos(n﹣1)α+i(sinnα﹣2sin(n﹣1)α)],再利用數列極限求和公式即可得出.


 導學全程練創優訓練系列答案
導學全程練創優訓練系列答案科目:高中數學 來源: 題型:
【題目】已知△ABC的內角A,B,C滿足sin2A+sin(A﹣B+C)=sin(C﹣A﹣B)+ ![]() ,面積S滿足1≤S≤2,記a,b,c分別為A,B,C所對的邊,在下列不等式一定成立的是( )
,面積S滿足1≤S≤2,記a,b,c分別為A,B,C所對的邊,在下列不等式一定成立的是( )
A.bc(b+c)>8
B.ab(a+b)>16 ![]()
C.6≤abc≤12
D.12≤abc≤24
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓 ![]() =1(a>b>0)的右焦點為F2(1,0),點H(2,
=1(a>b>0)的右焦點為F2(1,0),點H(2, ![]() )在橢圓上.
)在橢圓上.
(1)求橢圓的方程;
(2)點M在圓x2+y2=b2上,且M在第一象限,過M作圓x2+y2=b2的切線交橢圓于P,Q兩點,求證:△PF2Q的周長是定值.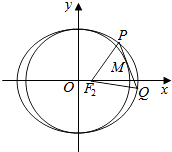
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】我國古代數學名著《九章算術》的論割圓術中有:“割之彌細,所失彌少,割之又割,以至于不可割,則與圓周合體而無所失矣.”它體現了一種無限與有限的轉化過程.比如在表達式1+ ![]() 中“…”即代表無數次重復,但原式卻是個定值,它可以通過方程1+
中“…”即代表無數次重復,但原式卻是個定值,它可以通過方程1+ ![]() =x求得x=
=x求得x= ![]() .類比上述過程,則
.類比上述過程,則 ![]() =( )
=( )
A.3
B.![]()
C.6
D.2 ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,點P在正方體ABCD﹣A1B1C1D1的表面上運動,且P到直線BC與直線C1D1的距離相等,如果將正方體在平面內展開,那么動點P的軌跡在展開圖中的形狀是( )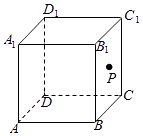
A.
B.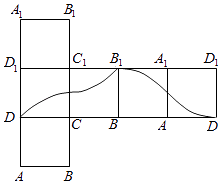
C.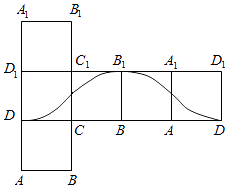
D.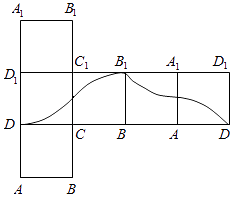
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,焦點在x軸的橢圓,離心率e= ![]() ,且過點A(﹣2,1),由橢圓上異于點A的P點發出的光線射到A點處被直線y=1反射后交橢圓于Q點(Q點與P點不重合).
,且過點A(﹣2,1),由橢圓上異于點A的P點發出的光線射到A點處被直線y=1反射后交橢圓于Q點(Q點與P點不重合).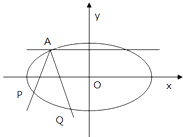
(1)求橢圓標準方程;
(2)求證:直線PQ的斜率為定值;
(3)求△OPQ的面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在直四棱柱ABCD﹣A1B1C1D1中,底面ABCD為等腰梯形,AB∥CD,AB=4,BC=CD=2,AA1=2,E、F、G分別是棱A1B1、AB、A1D1的中點.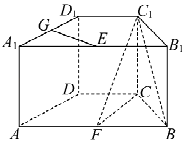
(Ⅰ)求證:GE⊥平面FCC1;
(Ⅱ)求二面角B﹣FC1﹣C的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在平面四邊形ABCD中,已知∠A= ![]() ,∠B=
,∠B= ![]() ,AB=6.在AB邊上取點E使得BE=1,連結EC,ED,若∠CED=
,AB=6.在AB邊上取點E使得BE=1,連結EC,ED,若∠CED= ![]() ,EC=
,EC= ![]() .則CD= .
.則CD= . 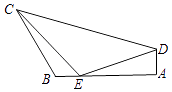
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com