
【題目】已知橢圓![]() 的左、右焦點分別為
的左、右焦點分別為![]() ,短軸兩個端點為
,短軸兩個端點為![]() ,且四邊形
,且四邊形![]() 是邊長為2的正方形.
是邊長為2的正方形.
(1)求橢圓的方程;
(2)若![]() 分別是橢圓長軸的左、右端點,動點
分別是橢圓長軸的左、右端點,動點![]() 滿足
滿足![]() ,連結
,連結![]() ,交橢圓于點
,交橢圓于點![]() ,證明:
,證明:![]() 為定值;
為定值;
(3)在(2)的條件下,試問![]() 軸上是否存在異于點
軸上是否存在異于點![]() 的定點
的定點![]() ,使得以
,使得以![]() 為直徑的圓恒過直線
為直徑的圓恒過直線![]() 的交點,若存在,求出點
的交點,若存在,求出點![]() 的坐標;若不存在,說明理由.
的坐標;若不存在,說明理由.
科目:高中數學 來源: 題型:
【題目】如圖,某城市有一塊半徑為40 m的半圓形綠化區域(以O 為圓心,AB為直徑),現計劃對其進行改建.在AB的延長線上取點D,OD=80 m,在半圓上選定一點C,改建后的綠化區域由扇形區域AOC和三角形區域COD組成,其面積為S m2.設∠AOC=x rad.
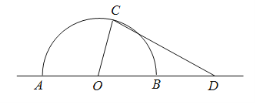
(1)寫出S關于x的函數關系式S(x),并指出x的取值范圍;
(2)試問∠AOC多大時,改建后的綠化區域面積S取得最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】根據國家環保部新修訂的《環境空氣質量標準》規定:居民區![]() 的年平均濃度不得超過
的年平均濃度不得超過![]() 微克/立方米,
微克/立方米,![]() 的24小時平均濃度不得超過
的24小時平均濃度不得超過![]() 微克/立方米.某城市環保部門隨機抽取了一居民區去年20天
微克/立方米.某城市環保部門隨機抽取了一居民區去年20天![]() 的24小時平均濃度的監測數據,數據統計如下:
的24小時平均濃度的監測數據,數據統計如下:
組別 |
(微克/立方米) | 頻數(天) | 頻率 |
第一組 |
| 3 | 0.15 |
第二組 |
| 12 | 0.6 |
第三組 |
| 3 | 0.15 |
第四組 |
| 2 | 0.1 |
(1)從樣本中![]() 的24小時平均濃度超過50微克/立方米的5天中,隨機抽取2天,求恰好有一天
的24小時平均濃度超過50微克/立方米的5天中,隨機抽取2天,求恰好有一天
![]() 的24小時平均濃度超過75微克/立方米的概率;
的24小時平均濃度超過75微克/立方米的概率;
(2)求樣本平均數,并根據樣本估計總體的思想,從![]() 的年平均濃度考慮,判斷該居民區的環境是
的年平均濃度考慮,判斷該居民區的環境是
否需要改進?說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列![]() 滿足
滿足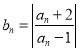 ,其中
,其中![]() ,
, ![]() .
.
(1)求![]() ,
, ![]() ,
, ![]() ,并猜想
,并猜想![]() 的表達式(不必寫出證明過程);
的表達式(不必寫出證明過程);
(2)設![]() ,數列
,數列![]() 的前
的前![]() 項和為
項和為![]() ,求證:
,求證: ![]() .
.
(B)已知數列![]() 的前
的前![]() 項和為
項和為![]() ,且滿足
,且滿足![]() ,
, ![]() .
.
(1)求![]() ,
, ![]() ,
, ![]() ,
, ![]() ,并猜想
,并猜想![]() 的表達式(不必寫出證明過程);
的表達式(不必寫出證明過程);
(2)設![]() ,
, ![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知A(4,-3),B(2,-1)和直線l:4x+3y-2=0.
(1)求在直角坐標平面內滿足|PA|=|PB|的點P的方程;
(2)求在直角坐標平面內一點P滿足|PA|=|PB|且點P到直線l的距離為2的坐標.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com