Question

1．設(shè)x∈（0，π），函數(shù)f（x）=sin（cosx）-x，g（x）=cos（sinx）-x．則下列說(shuō)法正確的是（　　）

• A． f（x），g（x）均有零點(diǎn)
• B． f（x），g（x）都沒(méi)有有零點(diǎn)
• C． g（x）有，f（x）沒(méi)有
• D． f（x）有，g（x）沒(méi)有

Answer 1

分析 畫(huà)出兩個(gè)函數(shù)的圖象即可判斷函數(shù)零點(diǎn)時(shí)分存在，推出結(jié)論．

解答 解：x∈（0，π），函數(shù)f（x）=sin（cosx）-x，g（x）=cos（sinx）-x．的圖象如圖：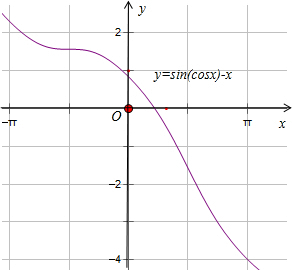

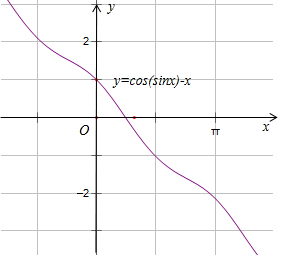
f（0）=sin1＞0，f（$\frac{π}{2}$）=-$\frac{π}{2}$＜0，函數(shù)f（x）有零點(diǎn)；
g（0）=1＞0，g（$\frac{π}{2}$）=cos1-$\frac{π}{2}$＜0，函數(shù)g（x）有零點(diǎn)；
故選：A．

點(diǎn)評(píng) 本題考查函數(shù)的零點(diǎn)判定定理的應(yīng)用，考查計(jì)算能力．