
【題目】已知函數![]() .
.
(1)當![]() 時,
時,
①若曲線![]() 與直線
與直線![]() 相切,求
相切,求![]() 的值;
的值;
②若曲線![]() 與直線
與直線![]() 有公共點,求
有公共點,求![]() 的取值范圍.
的取值范圍.
(2)當![]() 時,不等式
時,不等式![]() 對于任意正實數
對于任意正實數![]() 恒成立,當
恒成立,當![]() 取得最大值時,求
取得最大值時,求![]() 的值.
的值.
【答案】(1)①1 ,②![]() ;(2)1,-1.
;(2)1,-1.
【解析】
![]() 當
當![]() 時,
時,![]() ,所以
,所以![]() ,
,
① 設切點為![]() ,列出方程組,即可求得
,列出方程組,即可求得![]() ,得到答案
,得到答案
②由題意,得方程![]() 有正實數根,即方程
有正實數根,即方程![]() 有正實數根,記
有正實數根,記![]() ,利用導數求得函數的單調性和最小值,即可求解
,利用導數求得函數的單調性和最小值,即可求解![]() 的取值范圍
的取值范圍
![]() 由題意得,當
由題意得,當![]() 時,
時,![]() 對于任意正實數
對于任意正實數![]() 恒成立,所以當
恒成立,所以當![]() 時,
時,![]() 對于任意正實數
對于任意正實數![]() 恒成立,由
恒成立,由![]() 知,
知,![]() ,進而得到
,進而得到![]() ,
,
![]() ,
,![]() ,……,得到當
,……,得到當![]() 時,
時,![]() ,進而得到
,進而得到![]() 對于任意正實數
對于任意正實數![]() 恒成立,再利用二次函數的性質,即可得到結論
恒成立,再利用二次函數的性質,即可得到結論
(1)解:當![]() 時,
時,![]() ,所以
,所以![]() .
.
①設切點為![]() ,則
,則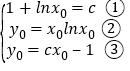
由②③得,![]()
由①得![]() 代入④得,
代入④得,![]()
所以![]() .
.
②由題意,得方程![]() 有正實數根,
有正實數根,
即方程![]() 有正實數根,
有正實數根,
記![]() ,令
,令![]() ,
,
當![]() 時,
時,![]() ;當
;當![]() 時,
時,![]() ;
;
所以![]() 在
在![]() 上為減函數,在
上為減函數,在![]() 上為增函數;
上為增函數;
所以![]() .
.
若![]() ,則
,則![]() ,不合;
,不合;
若![]() ,由①知適合;
,由①知適合;
若![]() ,則
,則![]() ,又
,又![]() ,
,
所以![]() ,由零點存在性定理知
,由零點存在性定理知![]() 在
在![]() 上必有零點.
上必有零點.
綜上,c的取值范圍為![]() .
.
(2)由題意得,當![]() 時,
時,![]() 對于任意正實數x恒成立,
對于任意正實數x恒成立,
所以當![]() 時,
時,![]() 對于任意正實數x恒成立,
對于任意正實數x恒成立,
由(1)知,![]() ,
,
兩邊同時乘以x得,![]() ①
①
兩邊同時加上![]() 得,
得,![]() ②,
②,
所以![]() (*),當且僅當
(*),當且僅當![]() 時取等號.
時取等號.
對(*)式重復以上步驟①②可得,![]() ,
,
進而可得,![]() ,
,![]() ,……,
,……,
所以當![]() ,
,![]() 時,
時,![]() ,當且僅當
,當且僅當![]() 時取等號.
時取等號.
所以![]() .
.
當![]() 取最大值1時,
取最大值1時,![]()
令上式中![]() 得,
得, ![]() ,所以
,所以![]() ,
,
所以![]() 對于任意正實數x恒成立,
對于任意正實數x恒成立,
即![]() 對于任意正實數x恒成立,
對于任意正實數x恒成立,
所以![]() ,所以函數
,所以函數![]() 的對稱軸
的對稱軸![]() ,
,
所以![]() ,即
,即![]() ,所以
,所以![]() ,
,![]() .
.
又由![]() ,兩邊同乘以x2得,
,兩邊同乘以x2得,![]() ,
,
所以當![]() ,
,![]() 時,
時,![]() 也恒成立,
也恒成立,
綜上,得![]() ,
,![]() .
.


科目:高中數學 來源: 題型:
【題目】如圖,四邊形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分別在
分別在![]() ,
,![]() 上,
上,![]() ,現將四邊形
,現將四邊形![]() 沿
沿![]() 折起,使平面
折起,使平面![]() 平面
平面![]() .
.
(Ⅰ)若![]() ,在折疊后的線段
,在折疊后的線段![]() 上是否存在一點
上是否存在一點![]() ,且
,且![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,說明理由;
的值;若不存在,說明理由;
(Ⅱ)當三棱錐![]() 的體積最大時,求二面角
的體積最大時,求二面角![]() 的余弦值.
的余弦值.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】現對一塊長![]() 米,寬
米,寬![]() 米的矩形場地ABCD進行改造,點E為線段BC的中點,點F在線段CD或AD上(異于A,C),設
米的矩形場地ABCD進行改造,點E為線段BC的中點,點F在線段CD或AD上(異于A,C),設![]() (單位:米),
(單位:米),![]() 的面積記為
的面積記為![]() (單位:平方米),其余部分面積記為
(單位:平方米),其余部分面積記為![]() (單位:平方米).
(單位:平方米).
(1)求函數![]() 的解析式;
的解析式;
(2)設該場地中![]() 部分的改造費用為
部分的改造費用為![]() (單位:萬元),其余部分的改造費用為
(單位:萬元),其余部分的改造費用為![]() (單位:萬元),記總的改造費用為W單位:萬元),求W最小值,并求取最小值時x的值.
(單位:萬元),記總的改造費用為W單位:萬元),求W最小值,并求取最小值時x的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在三棱柱ABC-A1B1C1中,BB1⊥平面ABC,∠BAC=90°,AC=AB=AA1,E是BC的中點.

(1)求證:AE⊥B1C;
(2)求異面直線AE與A1C所成的角的大小;
(3)若G為C1C中點,求二面角C-AG-E的正切值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司一年需購買某種原料400噸,設公司每次都購買![]() 噸,每次運費為4萬元,一年的總存儲費用為
噸,每次運費為4萬元,一年的總存儲費用為![]() 萬元.
萬元.
(1)要使一年的總運費與總存儲費用之和最小,則每次購買多少噸?
(2)要使一年的總運費與總存儲費用之和不超過200萬元,則每次購買量在什么范圍?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2017高考特別強調了要增加對數學文化的考查,為此某校高三年級特命制了一套與數學文化有關的專題訓練卷(文、理科試卷滿分均為100分),并對整個高三年級的學生進行了測試.現從這些學生中隨機抽取了50名學生的成績,按照成績為![]() ,
, ![]() ,…,
,…, ![]() 分成了5組,制成了如圖所示的頻率分布直方圖(假定每名學生的成績均不低于50分).
分成了5組,制成了如圖所示的頻率分布直方圖(假定每名學生的成績均不低于50分).
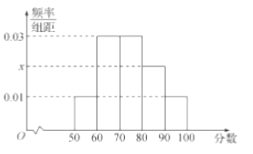
(1)求頻率分布直方圖中的![]() 的值,并估計所抽取的50名學生成績的平均數、中位數(同一組中的數據用該組區間的中點值代表);
的值,并估計所抽取的50名學生成績的平均數、中位數(同一組中的數據用該組區間的中點值代表);
(2)若高三年級共有2000名學生,試估計高三學生中這次測試成績不低于70分的人數;
(3)若在樣本中,利用分層抽樣的方法從成績不低于70分的三組學生中抽取6人,再從這6人中隨機抽取3人參加這次考試的考后分析會,試求![]() 兩組中至少有1人被抽到的概率.
兩組中至少有1人被抽到的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】按照國家質量標準:某種工業產品的質量指標值落在[100,120)內,則為合格品,否則為不合格品.某企業有甲乙兩套設備生產這種產品,為了檢測這兩套設備的生產質量情況,隨機從兩套設備生產的大量產品中各抽取了50件產品作為樣本對規定的質量指標值進行檢測.表1是甲套設備的樣本頻數分布表,圖1是乙套設備的樣本頻率分布直方圖.

質量指標值 | [95,100) | [100,105) | [105,110) | [110,115) | [115,120) | [120,125] |
頻數 | 1 | 4 | 19 | 20 | 5 | 1 |
表1:甲套設備的樣本頻數分布表
(1)將頻率視為概率,若乙套設備生產了5000件產品,則其中合格品約有多少件?
(2)填寫下面2×2列聯表,并根據列聯表判斷是否有95%的把握認為這種產品的質量指標值與甲乙兩套設備的選擇有關:
甲套設備 | 乙套設備 | 合計 | |
合格品 | |||
不合格品 | |||
合計 |
(3)根據表和圖,對甲、乙兩套設備的優劣進行比較.參考公式及數據:x2=![]()
P(Х2≥k) | 0.100 | 0.050 | 0.010 |
k | 2.706 | 3.841 | 6.635 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com