
【題目】若![]() ,當x∈[0,1]時,f(x)=x,若在區間(﹣1,1]內,
,當x∈[0,1]時,f(x)=x,若在區間(﹣1,1]內,![]() 有兩個零點,則實數m的取值范圍是( )
有兩個零點,則實數m的取值范圍是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】B
【解析】
根據當x∈[0,1]時,f(x)=x,當x∈(﹣1,0)時,x+1∈(0,1),得到f(x)![]() ,故f(x)
,故f(x)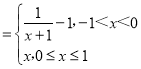 ,題目問題轉化為函數y=f(x)與函數y=m(x
,題目問題轉化為函數y=f(x)與函數y=m(x![]() )在區間(﹣1,1]內有兩個交點,在同一坐標系內畫出兩個函數的圖象,根據圖象,利用數形結合法即可求出m的取值范圍.
)在區間(﹣1,1]內有兩個交點,在同一坐標系內畫出兩個函數的圖象,根據圖象,利用數形結合法即可求出m的取值范圍.
根據題意,![]() ,又當x∈[0,1]時,f(x)=x,
,又當x∈[0,1]時,f(x)=x,
故當x∈(﹣1,0)時,x+1∈(0,1),則f(x)+1![]() ,
,
所以f(x)![]() ,
,
故f(x)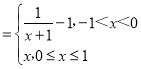 ,
,
因為![]() 在區間(﹣1,1]內有兩個零點,
在區間(﹣1,1]內有兩個零點,
所以方程f(x)=m(x![]() )在區間(﹣1,1]內有兩個根,
)在區間(﹣1,1]內有兩個根,
所以函數y=f(x)與函數y=m(x![]() )在區間(﹣1,1]內有兩個交點,
)在區間(﹣1,1]內有兩個交點,
而函數y=m(x![]() )恒過定點(
)恒過定點(![]() ,0),在同一坐標系內畫出兩個函數的圖象,如圖所示:
,0),在同一坐標系內畫出兩個函數的圖象,如圖所示:
 ,
,
當y=m(x![]() )過點(1,1)時,斜率m
)過點(1,1)時,斜率m![]() ,
,
當y=m(x![]() )過點(1,0)時,斜率m=0,
)過點(1,0)時,斜率m=0,
由圖象可知,當0<m![]() 時,兩個函數圖象有兩個交點,
時,兩個函數圖象有兩個交點,
即![]() 有兩個零點,
有兩個零點,
故選:B.


科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的焦距為2,且長軸長是短軸長的
的焦距為2,且長軸長是短軸長的![]() 倍.
倍.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)若過橢圓![]() 左焦點
左焦點![]() 的直線
的直線![]() 交橢圓
交橢圓![]() 于
于![]() 兩點,點
兩點,點![]() 在
在![]() 軸非負半軸上,且點
軸非負半軸上,且點![]() 到坐標原點的距離為2,求
到坐標原點的距離為2,求![]() 取得最大值時
取得最大值時![]() 的面積.
的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知某企業近3年的前7個月的月利潤(單位:百萬元)如下面的折線圖所示:
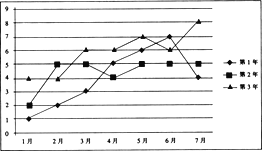
(1)試問這3年的前7個月中哪個月的月平均利潤最高?
(2)通過計算判斷這3年的前7個月的總利潤的發展趨勢;
(3)試以第3年的前4個月的數據(如下表),用線性回歸的擬合模式估測第3年8月份的利潤.
月份x | 1 | 2 | 3 | 4 |
利潤y(單位:百萬元) | 4 | 4 | 6 | 6 |
相關公式: 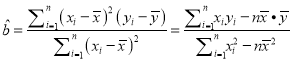 ,
, ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】多面體歐拉定理是指對于簡單多面體,其各維對象數總滿足一定的數量關系,在三維空間中,多面體歐拉定理可表示為:頂點數+表面數-棱長數=2.在數學上,富勒烯的結構都是以正五邊形和正六邊形面組成的凸多面體,例如富勒烯![]() (結構圖如圖)是單純用碳原子組成的穩定分子,具有60個頂點和32個面,其中12個為正五邊形,20個為正六邊形.除
(結構圖如圖)是單純用碳原子組成的穩定分子,具有60個頂點和32個面,其中12個為正五邊形,20個為正六邊形.除![]() 外具有封閉籠狀結構的富勒烯還可能有
外具有封閉籠狀結構的富勒烯還可能有![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,等,則
,等,則![]() 結構含有正六邊形的個數為( )
結構含有正六邊形的個數為( )

A.12B.24C.30D.32
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓C:![]() 的離心率為
的離心率為![]() ,與坐標軸分別交于A,B兩點,且經過點Q(
,與坐標軸分別交于A,B兩點,且經過點Q(![]() ,1).
,1).
(Ⅰ)求橢圓C的標準方程;
(Ⅱ)若P(m,n)為橢圓C外一動點,過點P作橢圓C的兩條互相垂直的切線l1、l2,求動點P的軌跡方程,并求△ABP面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系中,以坐標原點O為極點,x軸正半軸為極軸,建立極坐標系,點![]() ,(
,(![]() )在曲線C:
)在曲線C:![]() 上,直線l過點
上,直線l過點![]() 且與
且與![]() 垂直,垂足為P.
垂直,垂足為P.
(Ⅰ)當![]() 時,求在直角坐標系下點P坐標和l的方程;
時,求在直角坐標系下點P坐標和l的方程;
(Ⅱ)當M在C上運動且P在線段![]() 上時,求點P在極坐標系下的軌跡方程.
上時,求點P在極坐標系下的軌跡方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的長軸長為
的長軸長為![]() ,右頂點到左焦點的距離為
,右頂點到左焦點的距離為![]() ,
,![]() 、
、![]() 分別為橢圓
分別為橢圓![]() 的左、右兩個焦點.
的左、右兩個焦點.
(1)求橢圓![]() 的方程;
的方程;
(2)已知橢圓![]() 的切線
的切線![]() (與橢圓
(與橢圓![]() 有唯一交點)的方程為
有唯一交點)的方程為![]() ,切線
,切線![]() 與直線
與直線![]() 和直線
和直線![]() 分別交于點
分別交于點![]() 、
、![]() ,求證:
,求證:![]() 為定值,并求此定值;
為定值,并求此定值;
(3)設矩形![]() 的四條邊所在直線都和橢圓
的四條邊所在直線都和橢圓![]() 相切(即每條邊所在直線與橢圓
相切(即每條邊所在直線與橢圓![]() 有唯一交點),求矩形
有唯一交點),求矩形![]() 的面積
的面積![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在三棱錐![]() 中,
中,![]() 是邊長為2的正三角形,
是邊長為2的正三角形,![]() 是等腰直角三角形,
是等腰直角三角形,![]() .
.
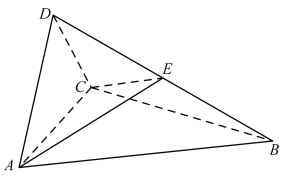
(I)證明:平面![]() 平面ABC;
平面ABC;
(II)點E在BD上,若平面ACE把三棱錐![]() 分成體積相等的兩部分,求二面角
分成體積相等的兩部分,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com