Question

7．如圖，已知四棱錐P-ABCD的底面是菱形，對角線AC，BD交于點O，OA=4，OB=3，OP=4，OP⊥底面ABCD，設點M滿足$\overrightarrow{PM}$=$\frac{1}{2}$$\overrightarrow{MC}$．
（1）求直線PA與平面BDM所成角的正弦值；
（2）求點P到平面BDM  的距離．

Answer 1

分析 （1）以O為坐標原點，以OA，OB，OP為坐標軸建立坐標系，求出平面BDM的法向量$\overrightarrow{n}$和$\overrightarrow{PA}$的坐標，則直線PA與平面BDM所成角的正弦值為|cos＜$\overrightarrow{PA}，\overrightarrow{n}$＞|；
（2）求出OP與平面BDM所成角的正弦值|cos＜$\overrightarrow{OP}，\overrightarrow{n}$＞|，則點P到平面BDM的距離為|OP||cos＜$\overrightarrow{OP}，\overrightarrow{n}$＞|．

解答 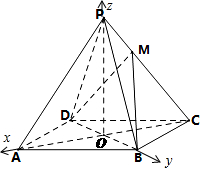解：（1）∵平面ABCD是菱形，∴AC⊥BD．
以O為坐標原點，以OA，OB，OP為坐標軸建立空間直角坐標系O-ABP如圖所示：
則A（4，0，0），B（0，3，0），C（-4，0，0），D（0，-3，0），P（0，0，4），
∴$\overrightarrow{PA}$=（4，0，-4），$\overrightarrow{DB}$=（0，6，0），$\overrightarrow{PC}$=（-4，0，-4），$\overrightarrow{BP}$=（0，-3，4）．
∵$\overrightarrow{PM}$=$\frac{1}{2}$$\overrightarrow{MC}$，∴$\overrightarrow{PM}$=$\frac{1}{3}$$\overrightarrow{PC}$=（-$\frac{4}{3}$，0，-$\frac{4}{3}$），$\overrightarrow{BM}$=$\overrightarrow{BP}+\overrightarrow{PM}$=（-$\frac{4}{3}$，-3，$\frac{8}{3}$）．
設平面BDM的法向量$\overrightarrow{n}$=（x，y，z），則$\left\{\begin{array}{l}{6y=0}\\{-\frac{4}{3}x-3y+\frac{8}{3}z=0}\end{array}\right.$，
令x=2，則z=1，∴平面BDM的一個法向量$\overrightarrow{n}$=（2，0，1），
∴cos＜$\overrightarrow{PA}，\overrightarrow{n}$＞=$\frac{\overrightarrow{PA}•\overrightarrow{n}}{|\overrightarrow{PA}||\overrightarrow{n}|}$=$\frac{4}{4\sqrt{2}×\sqrt{5}}$=$\frac{\sqrt{10}}{10}$，
∴直線PA與平面BDM所成角的正弦值為$\frac{\sqrt{10}}{10}$．
（ 2）$\overrightarrow{OP}$=（0，0，4），
∴cos＜$\overrightarrow{OP}，\overrightarrow{n}$＞=$\frac{\overrightarrow{OP}•\overrightarrow{n}}{|\overrightarrow{OP}||\overrightarrow{n}|}$=$\frac{4}{4×\sqrt{5}}$=$\frac{\sqrt{5}}{5}$，
∴OP與平面BDM所成角的正弦值為$\frac{\sqrt{5}}{5}$，
∴P到平面BDM的距離d=|OP|×$\frac{\sqrt{5}}{5}$=$\frac{4\sqrt{5}}{5}$．

點評 本題考查了線面角與線面距離的計算，空間向量在立體幾何中的應用，屬于中檔題．