
【題目】現有4個人參加某娛樂活動,該活動有甲、乙兩個游戲可供參加者選擇,為增加趣味性,約定:每個人通過擲一枚質地均勻的骰子決定自己去參加哪個游戲,擲出點數為1或2的人去參加甲游戲,擲出點數大于2的人去參加乙游戲.
(1) 求出4個人中恰有2個人去 參加甲游戲的概率;
(2)求這4個人中去參加甲游戲人數大于去參加乙游戲的人數的概率;
(3)用![]() 分別表示這4個人中去參加甲、乙游戲的人數,記
分別表示這4個人中去參加甲、乙游戲的人數,記![]() ,求隨機變量
,求隨機變量![]() 的分布列與數學期望
的分布列與數學期望![]() .
.
【答案】(1)8:27
(2)1:9
(3) ![]() 的分布列是
的分布列是
| 0 | 2 | 4 |
|
|
|
|
![]()
【解析】試題分析:依題意,這4個人中,每個人去參加甲游戲的概率為![]() ,去參加乙游戲的人數的概率為
,去參加乙游戲的人數的概率為![]() 設“這4個人中恰有i人去參加甲游戲”為事件
設“這4個人中恰有i人去參加甲游戲”為事件![]() ,故
,故![]() ;(Ⅰ)這4個人中恰有2人去參加甲游戲的概率為P(A2);(Ⅱ)設“這4個人中去參加甲游戲的人數大于去參加乙游戲”為事件B,則B=A3∪A4,利用互斥事件的概率公式可求;(Ⅲ)ξ的所有可能取值為0,2,4,由于A1與A3互斥,A0與A4互斥,求出相應的概率,可得ξ的分布列與數學期望.
;(Ⅰ)這4個人中恰有2人去參加甲游戲的概率為P(A2);(Ⅱ)設“這4個人中去參加甲游戲的人數大于去參加乙游戲”為事件B,則B=A3∪A4,利用互斥事件的概率公式可求;(Ⅲ)ξ的所有可能取值為0,2,4,由于A1與A3互斥,A0與A4互斥,求出相應的概率,可得ξ的分布列與數學期望.
試題解析:解:依題意,這4個人中,每個人去參加甲游戲的概率為![]() ,去參加乙游戲的概率為
,去參加乙游戲的概率為![]() .設“這4個人中恰有i人去參加甲游戲”為事件
.設“這4個人中恰有i人去參加甲游戲”為事件![]() (i=0,1,2,3,4),則
(i=0,1,2,3,4),則![]()
(Ⅰ)這4個人中恰有2人去參加甲游戲的概率![]() 3分
3分
(Ⅱ)設“這4個人中去參加甲游戲的人數大于去參加乙游戲的人數”為事件B,則![]() ,
,
由于![]() 與
與![]() 互斥,故
互斥,故![]()
所以,這4個人去參加甲游戲的人數大于去參加乙游戲的人數的概率為![]() 7分
7分
(Ⅲ)ξ的所有可能取值為0,2,4.由于![]() 與
與![]() 互斥,
互斥,![]() 與
與![]() 互斥,故
互斥,故
![]() ,
,![]()
![]() 。
。
所以ξ的分布列是
ξ | 0 | 2 | 4 |
P |
|
|
|
隨機變量ξ的數學期望![]() 12分.
12分.


科目:高中數學 來源: 題型:
【題目】在平面直角坐標系中,以原點為極點, ![]() 軸正半軸為極軸建立極坐標系,并在兩坐標系中取相同的長度單位.已知曲線
軸正半軸為極軸建立極坐標系,并在兩坐標系中取相同的長度單位.已知曲線![]() 的極坐標方程為
的極坐標方程為![]() ,直線
,直線![]() 的參數方程為
的參數方程為
![]() (
(![]() 為參數,
為參數, ![]() 為直線的傾斜角).
為直線的傾斜角).
(1)寫出直線![]() 的普通方程和曲線
的普通方程和曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)若直線![]() 與曲線
與曲線![]() 有唯一的公共點,求角
有唯一的公共點,求角![]() 的大小.
的大小.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】給出下列命題:①定義在![]() 上的函數
上的函數![]() 滿足
滿足![]() ,則
,則![]() 一定不是
一定不是![]() 上的減函數;
上的減函數;
②用反證法證明命題“若實數![]() ,滿足
,滿足![]() ,則
,則![]() 都為0”時,“假設命題的結論不成立”的敘述是“假設
都為0”時,“假設命題的結論不成立”的敘述是“假設![]() 都不為0”;
都不為0”;
③把函數![]() 的圖象向右平移
的圖象向右平移![]() 個單位長度,所得到的圖象的函數解析式為
個單位長度,所得到的圖象的函數解析式為![]() ;
;
④“![]() ”是“函數
”是“函數![]() 為奇函數”的充分不必要條件.
為奇函數”的充分不必要條件.
其中所有正確命題的序號為__________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某中學為研究學生的身體素質與課外體育鍛煉時間的關系,對400名高一學生的一周課外體育鍛煉時間進行調查,結果如下表所示:現采用分層抽樣的方法抽取容量為20的樣本.
(1)其中課外體育鍛煉時間在![]() 分鐘內的學生應抽取多少人?
分鐘內的學生應抽取多少人?
(2)若從(1)中被抽取的學生中隨機抽取2名,求這2名學生課外體育鍛煉時間均在![]() 分鐘內的概率.
分鐘內的概率.
鍛煉時間(分鐘) |
|
|
|
|
|
|
人數 | 40 | 60 | 80 | 100 | 80 | 40 |
查看答案和解析>>
科目:高中數學 來源: 題型:
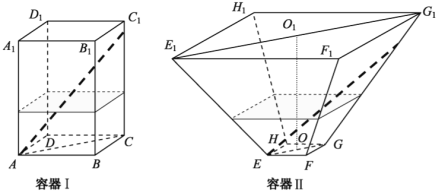
【題目】如圖,水平放置的正四棱柱形玻璃容器Ⅰ和正四棱臺形玻璃容器Ⅱ的高均為32cm,容器Ⅰ的底面對角線AC的長為10![]() cm,容器Ⅱ的兩底面對角線
cm,容器Ⅱ的兩底面對角線![]() ,
,![]() 的長分別為14cm和62cm.分別在容器Ⅰ和容器Ⅱ中注入水,水深均為12cm.現有一根玻璃棒l,其長度為40cm.(容器厚度、玻璃棒粗細均忽略不計)
的長分別為14cm和62cm.分別在容器Ⅰ和容器Ⅱ中注入水,水深均為12cm.現有一根玻璃棒l,其長度為40cm.(容器厚度、玻璃棒粗細均忽略不計)
(1)將![]() 放在容器Ⅰ中,
放在容器Ⅰ中,![]() 的一端置于點A處,另一端置于側棱
的一端置于點A處,另一端置于側棱![]() 上,求
上,求![]() 沒入水中部分的長度;
沒入水中部分的長度;
(2)將![]() 放在容器Ⅱ中,
放在容器Ⅱ中,![]() 的一端置于點E處,另一端置于側棱
的一端置于點E處,另一端置于側棱![]() 上,求
上,求![]() 沒入水中部分的長度.
沒入水中部分的長度.
查看答案和解析>>
科目:高中數學 來源: 題型:
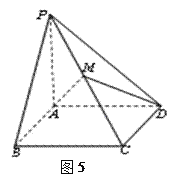
【題目】如圖5所示,已知四棱錐![]() 中,底面
中,底面![]() 為矩形,
為矩形, ![]() 底面
底面![]() ,
, ![]() ,
,
![]() ,
, ![]() 為
為![]() 的中點.
的中點.
⑴指出平面![]() 與
與![]() 的交點
的交點![]() 所在位置,并給出理由;
所在位置,并給出理由;
⑵求平面![]() 將四棱錐
將四棱錐![]() 分成上下兩部分的體積比.
分成上下兩部分的體積比.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com