
【題目】在四棱錐![]() 中,平面
中,平面![]() 平面
平面![]() ,側面
,側面![]() 是邊長為
是邊長為![]() 的等邊三角形,底面
的等邊三角形,底面![]() 是矩形,且
是矩形,且![]() ,則該四棱錐外接球的表面積等于__________.
,則該四棱錐外接球的表面積等于__________.
【答案】![]()
【解析】∵平面SAB⊥平面SAD,平面SAB∩平面SAD=SA,側面SAB是邊長為![]() 的等邊三角形,設AB的中點為E,SA的中點為F,
的等邊三角形,設AB的中點為E,SA的中點為F,
則BF⊥SA,∴BF⊥平面SAD,∴BF⊥AD,底面ABCD是矩形,∴AD⊥平面SAB,SE平面SAB,
∴AD⊥SE,又SE⊥AB,AB∩AD=A,
∴SE⊥底面ABCD,作圖如下:
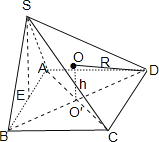
∵SAB是邊長為![]() 的等邊三角形,
的等邊三角形,
∴![]() .
.
又底面ABCD是矩形,且BC=4,
∴矩形ABCD的對角線長為![]() ,
,
∴矩形ABCD的外接圓的半徑為![]() .
.
設該四棱錐外接球的球心為O,半徑為R,O到底面的距離為h,
則r2+h2=R2,即7+h2=R2,又R2=22+(SEh)2=4+(3h)2,
∴7+h2=4+(3h)2,
∴h=1.
∴R2=7+h2=8,
∴該四棱錐外接球的表面積![]() .
.


科目:高中數學 來源: 題型:
【題目】我國古代數學名著《算法統宗》中有如下問題:“遠望巍巍塔七層,紅光點點倍加增,共燈三百八十一,請問尖頭幾盞燈?”意思是:一座7層塔共掛了381盞燈,且相鄰兩層中的下一層燈數是上一層燈數的2倍,則塔的頂層共有燈( )
A. 1盞 B. 3盞 C. 5盞 D. 9盞
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司為了準確地把握市場,做好產品生產計劃,對過去四年的數據進行整理得到了第![]() 年與年銷量
年與年銷量![]() (單位:萬件)之間的關系如下表:
(單位:萬件)之間的關系如下表:

(1)在圖中畫出表中數據的散點圖;
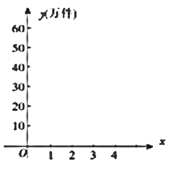
(2)根據散點圖選擇合適的回歸模型擬合![]() 與
與![]() 的關系(不必說明理由);
的關系(不必說明理由);
(3)建立![]() 關于
關于![]() 的回歸方程,預測第5年的銷售量.
的回歸方程,預測第5年的銷售量.
附注:參考公式:回歸直線的斜率和截距的最小二乘法估計公式分別為:
 ,
, ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=lg ![]() ,f(1)=0,且f(2)﹣f(
,f(1)=0,且f(2)﹣f( ![]() )=lg2.
)=lg2.
(1)求f(x)的表達式;
(2)若x∈(0,+∞)時方程f(x)=lgt有解,求實數t的取值范圍;
(3)若函數y=f(x)﹣lg(8x+m)的無零點,求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,三棱柱![]() 中,底面
中,底面![]() 為正三角形,
為正三角形, ![]() 底面
底面![]() ,且
,且![]() ,
, ![]() 是
是![]() 的中點.
的中點.
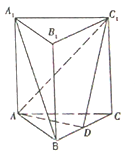
(1)求證: ![]() 平面
平面![]() ;
;
(2)求證:平面![]() 平面
平面![]() ;
;
(3)在側棱![]() 上是否存在一點
上是否存在一點![]() ,使得三棱錐
,使得三棱錐![]() 的體積是
的體積是![]() ?若存在,求出
?若存在,求出![]() 的長;若不存在,說明理由.
的長;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在△ABC中,a,b,c分別為內角A,B,C的對邊,且2asinA=(2b+c)sinB+(2c+b)sinC. (Ⅰ)求A的大小;
(Ⅱ)求sinB+sinC的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某市出租車的計價標準是:4km以內(含4km)10元,超過4km且不超過18km的部分1.2元/km,超過18km的部分1.8元/km,不計等待時間的費用.
(1)如果某人乘車行駛了10km,他要付多少車費?
(2)試建立車費y(元)與行車里程x(km)的函數關系式.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com