
【題目】已知函數f(x)=lg ![]() ,f(1)=0,且f(2)﹣f(
,f(1)=0,且f(2)﹣f( ![]() )=lg2.
)=lg2.
(1)求f(x)的表達式;
(2)若x∈(0,+∞)時方程f(x)=lgt有解,求實數t的取值范圍;
(3)若函數y=f(x)﹣lg(8x+m)的無零點,求實數m的取值范圍.
【答案】
(1)解:∵且f(2)﹣f( ![]() )=lg2,即x>0時,f(x)﹣f(
)=lg2,即x>0時,f(x)﹣f( ![]() )=lgx.
)=lgx.
lg ![]() ﹣lg
﹣lg ![]() =lgx,
=lgx,
即lg﹣lg=lgx,
即lg( ![]()
![]() )=lgx,
)=lgx, ![]()
![]() =x.
=x.
整理得(a﹣b)x2﹣(a﹣b)x=0恒成立,
∴a=b,
又f(1)=0,
即a+b=2,從而a=b=1.
∴f(x)=lg ![]() ,
,
∵ ![]() >0,
>0,
∴x<﹣1,或x>0,
∴f(x)的定義域為(﹣∞,﹣1)∪(0,+∞)
(2)解:方程f(x)=lgt有解,
即lg ![]() =lgt,
=lgt,
∴t= ![]() ,
,
∴x(2﹣t)=t,
∴x= ![]() ,
,
∴ ![]() <﹣1,或
<﹣1,或 ![]() >0,
>0,
解得t>2,或0<t<2,
∴實數t的取值范圍(0,2)∪(2,+∞)
(3)解:函數y=f(x)﹣lg(8x+m)的無零點即方程f(x)=lg(8x+m)的解集為,
∴lg ![]() =lg(8x+m),
=lg(8x+m),
∴ ![]() =8x+m,
=8x+m,
∴8x2+(6+m)x+m=0,
方程的解集為,故有兩種情況:
①方程8x2+(6+m)x+m=0無解,即△<0,得2<m<18,
②方程8x2+(6+m)x+m=0有解,兩根均在[﹣1,0]內,g(x)=8x2+(6+m)x+m,
則 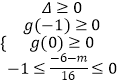 ,解得:0≤m≤2,
,解得:0≤m≤2,
綜合①②得實數m的取值范圍是0≤m<18
【解析】(1)由已知中函數,以構造一個關于a,b方程組,解方程組求出a,b值,進而得到f(x)的表達式;(2)由(1)中函數f(x)的表達式,轉化為一個方程,分離參數,根據f(x)的定義域即可求出;(3)根據對數的運算性質,可將方程f(x)=lg(8x+m),轉化為一個關于x的分式方程組,進而根據方程f(x)=lg(8x+m)的解集為,則方程組至少一個方程無解,或兩個方程的解集的交集為空集,分類討論后,即可得到答案.


 口算能手系列答案
口算能手系列答案科目:高中數學 來源: 題型:
【題目】如圖是2017年第一季度五省![]() 情況圖,則下列陳述正確的是( )
情況圖,則下列陳述正確的是( )
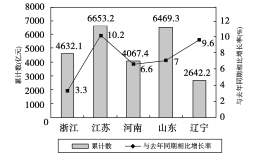
①2017年第一季度 ![]() 總量和增速均居同一位的省只有1個;
總量和增速均居同一位的省只有1個;
②與去年同期相比,2017年第一季度五個省的![]() 總量均實現了增長;
總量均實現了增長;
③去年同期的![]() 總量前三位是江蘇、山東、浙江;
總量前三位是江蘇、山東、浙江;
④2016年同期浙江的![]() 總量也是第三位.
總量也是第三位.
A. ①② B. ②③④ C. ②④ D. ①③④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() (
(![]() ),的兩個焦點
),的兩個焦點![]() ,
, ![]() ,點
,點![]() 在此橢圓上.
在此橢圓上.
(1)求橢圓![]() 的方程;
的方程;
(2)過點![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 相交于
相交于![]() 兩點,設點
兩點,設點![]() ,記直線
,記直線![]() 的斜率分別為
的斜率分別為![]() ,求證:
,求證: ![]() 為定值.
為定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校高三年級共有學生195人,其中女生105人,男生90人.現采用按性別分層抽樣的方法,從中抽取13人進行問卷調查.設其中某項問題的選擇分別為“同意”、“不同意”兩種,且每人都做了一種選擇.下面表格中提供了被調查人答卷情況的部分信息.
同意 | 不同意 | 合計 | |
女學生 | 4 | ||
男學生 | 2 |
(Ⅰ)完成上述統計表;
(Ⅱ)根據上表的數據估計高三年級學生該項問題選擇“同意”的人數;
(Ⅲ) 從被抽取的女生中隨機選取2人進行訪談,求選取的2名女生中至少有一人選擇“同意”的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com