
【題目】如圖,在直角梯形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() .直角梯形
.直角梯形![]() 通過直角梯形
通過直角梯形![]() 以直線
以直線![]() 為軸旋轉得到,且使平面
為軸旋轉得到,且使平面![]() 平面
平面![]() .
. ![]() 為線段
為線段![]() 的中點,
的中點, ![]() 為線段
為線段![]() 上的動點.
上的動點.

(1)求證: ![]() ;
;
(2)當點![]() 是線段
是線段![]() 中點時,求二面角
中點時,求二面角![]() 的余弦值;
的余弦值;
(3)是否存在點![]() ,使得直線
,使得直線![]() 平面
平面![]() ?請說明理由.
?請說明理由.
【答案】(1)見解析(2) ![]() (3)存在點
(3)存在點![]() ,使得直線
,使得直線![]() 平面
平面![]()
【解析】試題分析:(Ⅰ)由![]() 平面
平面![]() 平面
平面![]() ..推出
..推出![]() 平面
平面![]() .即可證明
.即可證明![]() .
.
(Ⅱ)以AC,AB,AA1為x軸、y軸、z軸建立空間直角坐標系,求出平面ABM的一個法向量,平面APM的一個法向量,利用空間向量的數量積求解二面角P﹣AM﹣B的余弦值.
(Ⅲ)存在點P,使得直線A1C∥平面AMP.設P(x1,y1,z1),求出平面AMP的一個法向量,求出![]() ,利用
,利用![]() .求出λ,即可證明結果.
.求出λ,即可證明結果.
試題解析:
(1)由已知![]() ,平面
,平面![]() 平面
平面![]()
![]() 平面
平面![]() ,平面
,平面![]()
![]() 平面
平面![]()
所以![]() 平面
平面![]()
又![]() 平面
平面![]()
所以![]()
(2)由(1)可知![]() ,
, ![]() ,
, ![]() 兩兩垂直.
兩兩垂直.
分別以![]() ,
, ![]() ,
, ![]() 為
為![]() 軸,
軸, ![]() 軸,
軸, ![]() 軸建立空間直角坐標系如圖所示.
軸建立空間直角坐標系如圖所示.
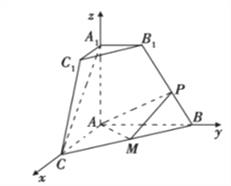
由已知![]()
![]()
所以![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]()
因為![]() 為線段
為線段![]() 的中點,
的中點, ![]() 為線段
為線段![]() 的中點.
的中點.
所以![]() ,
, ![]()
易知平面![]() 的一個法向量
的一個法向量![]()
設平面![]() 的一個法向量為
的一個法向量為![]()
由![]() 得
得
取![]() ,得
,得![]()
由圖可知,二面角![]() 的大小為銳角,
的大小為銳角,
所以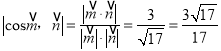
所以二面角![]() 的余弦值為
的余弦值為![]()
(3)存在點![]() ,使得直線
,使得直線![]() 平面
平面![]()
設![]() ,且
,且![]() ,
, ![]() ,則
,則![]()
所以![]() ,
, ![]() ,
, ![]() .所以
.所以![]()
設平面![]() 的一個法向量為
的一個法向量為![]() ,
,
由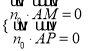 得
得![]()
取![]() ,得
,得![]() (
(![]() 不符合題意)
不符合題意)
又![]() 若
若![]() 平面
平面![]() ,則
,則![]()
所以![]() ,所以
,所以![]()
所以存在點![]() ,使得直線
,使得直線![]() 平面
平面![]()


科目:高中數學 來源: 題型:
【題目】已知圓C1:x2+y2-4x-2y-5=0與圓C2:x2+y2-6x-y-9=0.
(1)求證:兩圓相交;(2)求兩圓公共弦所在的直線方程;
(3)在平面上找一點P,過P點引兩圓的切線并使它們的長都等于![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,四邊形ABCD是平行四邊形,平面AED⊥平面ABNCD,EF∥AB,AB=2,BC=EF=1,AE= ![]() ,∠BAD=60°,G為BC的中點.
,∠BAD=60°,G為BC的中點. 
(1)求證:FG∥平面BED;
(2)求證:平面BED⊥平面AED;
(3)求直線EF與平面BED所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在三棱錐V﹣ABC中,平面VAB⊥平面ABC,△VAB為等邊三角形,AC⊥BC且AC=BC=![]() ,O,M分別為AB,VA的中點.
,O,M分別為AB,VA的中點.
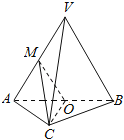
(1)求證:VB∥平面MOC;
(2)求證:平面MOC⊥平面VAB
(3)求三棱錐V﹣ABC的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列幾個命題
①方程![]() 有一個正實根,一個負實根,則
有一個正實根,一個負實根,則![]() ;
;
②函數![]() 是偶函數,但不是奇函數;
是偶函數,但不是奇函數;
③命題“若![]() ,則
,則![]() ”的否命題為“若
”的否命題為“若![]() ,則
,則![]() ”;
”;
④命題“![]() ,使得
,使得![]() ”的否定是“
”的否定是“![]() ,都有
,都有![]() ”;
”;
⑤“![]() ”是“
”是“![]() ”的充分不必要條件.
”的充分不必要條件.
正確的是__________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=x2+bx,則“b<0”是“f(f(x))的最小值與f(x)的最小值相等”的( )
A.充分不必要條件
B.必要不充分條件
C.充分必要條件
D.既不充分也不必要條件
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓心在![]() 軸上的圓
軸上的圓![]() 與直線
與直線![]() 切于點
切于點![]() .圓
.圓![]() :
: ![]() .
.
(1)求圓![]() 的標準方程;
的標準方程;
(2)已知![]() ,圓
,圓![]() 與
與![]() 軸相交于兩點
軸相交于兩點![]() (點
(點![]() 在點
在點![]() 的右側).過點
的右側).過點![]() 任作一條傾斜角不為0的直線與圓
任作一條傾斜角不為0的直線與圓![]() 相交于
相交于![]() 兩點.問:是否存在實數
兩點.問:是否存在實數![]() ,使得
,使得![]() ?若存在,求出實數
?若存在,求出實數![]() 的值,若不存在,請說明理由.
的值,若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com