
已知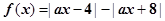 ,
,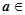 R
R
(Ⅰ)當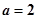 時,解不等式
時,解不等式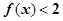 ;
;
(Ⅱ)若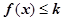 恒成立,求k的取值范圍.
恒成立,求k的取值范圍.
(Ⅰ){x|x>-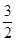 };(Ⅱ)[12,+∞).
};(Ⅱ)[12,+∞).
解析試題分析:(Ⅰ)利用分類討論思想將函數轉化為分段函數,然后逐一求解每個不等式;(Ⅱ)利用絕對值性質定理求解f(x)=|ax-4|-|ax+8|的最大值,然后確定k的取值范圍.
試題解析:(Ⅰ)當a=2時,
f(x)=2(|x-2|-|x+4|)=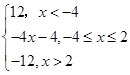
當x<-4時,不等式不成立;
當-4≤x≤2時,由-4x-4<2,得-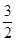 <x≤2;
<x≤2;
當x>2時,不等式必成立.
綜上,不等式f(x)<2的解集為{x|x>-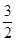 }.
}.
(Ⅱ)因為f(x)=|ax-4|-|ax+8|≤|(ax-4)-(ax+8)|=12,
當且僅當ax≤-8時取等號.
所以f(x)的最大值為12.
故k的取值范圍是[12,+∞).
考點:1.絕對值不等式的解法;2.絕對值不等式的性質定理.


科目:高中數學 來源: 題型:解答題
已知函數f(x)=|x-2|+2|x-a|(a∈R).
(I)當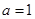 時,解不等式f(x)>3;
時,解不等式f(x)>3;
(II)不等式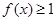 在區間(-∞,+∞)上恒成立,求實數a的取值范圍.
在區間(-∞,+∞)上恒成立,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
在平面直角坐標系xOy中,將從點M出發沿縱、橫方向到達點N的任一路徑成為M到N的一條“L路徑”。如圖所示的路徑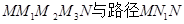 都是M到N的“L路徑”。某地有三個新建的居民區,分別位于平面xOy內三點
都是M到N的“L路徑”。某地有三個新建的居民區,分別位于平面xOy內三點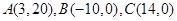 處。現計劃在x軸上方區域(包含x軸)內的某一點P處修建一個文化中心。
處。現計劃在x軸上方區域(包含x軸)內的某一點P處修建一個文化中心。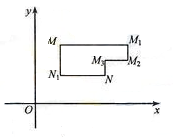
(I)寫出點P到居民區A的“L路徑”長度最小值的表達式(不要求證明);
(II)若以原點O為圓心,半徑為1的圓的內部是保護區,“L路徑”不能進入保護區,請確定點P的位置,使其到三個居民區的“L路徑”長度值和最小。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com