【題目】已知 
=（1，2）， 
=（﹣3，2），當k為何值時：
（1）k + 與 ﹣3 垂直；
（2）k + 與 ﹣3 平行，平行時它們是同向還是反向？
【答案】
（1）解：由題意可得 k 
+ 
=（k﹣3，2k+2）， ﹣3 =（10，﹣4），
由 k + 與 ﹣3 垂直可得 （k﹣3，2k+2）（10，﹣4）=10（k﹣3）+（2k+2）（﹣4）=0，解得k=19．
（2）解：由 k + 與 ﹣3 平行，可得（k﹣3）（﹣4）﹣（2k+2）×10=0，解得k=﹣ 
，
此時，k + =﹣ + =（﹣ 
， 
）， ﹣3 =（10，﹣4），顯然k + 與 ﹣3 方向相反．
【解析】（1）由題意可得 k + 和 ﹣3 的坐標，由 k + 與 ﹣3 垂直可得它們的數量積等于 0，由此解得k的值．（2）由 k + 與 ﹣3 平行的性質，可得（k﹣3）（﹣4）﹣（2k+2）×10=0，解得k的值．再根據 k + 和 ﹣3 的坐標，可得k + 與 ﹣3 方向相反．
科目：高中數學 來源： 題型：
【題目】已知點
，點
是圓
上的任意一點，設
為該圓的圓心，并且線段
的垂直平分線與直線
交于點
.
（1）求點
的軌跡方程；
（2）已知
兩點的坐標分別為
， 
，點
是直線
上的一個動點，且直線
分別交（1）中點
的軌跡于
兩點（
四點互不相同），證明：直線
恒過一定點，并求出該定點坐標.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】將函數y=sin2x的圖象向左平移 
個單位，再向上平移1個單位，所得圖象的函數解析式是（ ）
A.y=cos2x
B.y=2cos2x
C.
D.y=2sin2x?
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】正三棱臺的上、下底面的邊長分別是3和6．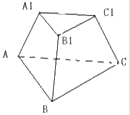 
（1）若側面與底面所成的角為60°，求此三棱臺的體積；
（2）若側棱與底面所成的角為60°，求此三棱臺的側面積．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
.
（1）討論函數
的單調性；
（2）當
時，若函數
的導函數
的圖象與
軸交于
， 
兩點，其橫坐標分別為
， 
，線段
的中點的橫坐標為
，且
， 
恰為函數
的零點，求證： 
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
