【題目】《九章算術》是我國古代的數學名著，書中對幾何學的研究比西方早一千多年.在該書中，將底面為直角三角形，且側棱垂直于底面的三棱柱稱為塹堵；將底面為矩形，一側棱垂直于底面的四棱錐稱為陽馬；將四個面均為直角三角形的四面體稱為鱉臑.如圖，在塹堵
中，
，
，鱉臑
的體積為2，則陽馬
外接球表面積的最小值為__________．
百年學典課時學練測系列答案科目：高中數學 來源： 題型：
【題目】手機作為客戶端越來越為人們所青睞，通過手機實現衣食住行消費已經成為一種主要的消費方式.在某市，隨機調查了200名顧客購物時使用手機支付的情況，得到如下的2×2列聯表，已知從使用手機支付的人群中隨機抽取1人，抽到青年的概率為
.
（I）根據已知條件完成2×2列聯表，并根據此資料判斷是否有99.5%的把握認為“市場購物用手機支付與年齡有關”？
2×2列聯表：
青年 | 中老年 | 合計 | |
使用手機支付 | 120 | ||
不使用手機支付 | 48 | ||
合計 | 200 |
（Ⅱ）現采用分層抽樣的方法從這200名顧客中按照“使用手機支付”和“不使用手機支付”抽取一個容量為10的樣本，再從中隨機抽取3人，求這三人中“使用手機支付”的人數的分布列及期望.
附：
| 0.05 | 0.025 | 0.010 | 0.005 |
| 3.841 | 5.024 | 6.635 | 7.879 |
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓
上任意一點到兩焦點
距離之和為
，離心率為
．
（1）求橢圓的標準方程；
（2）若直線
的斜率為
，直線
與橢圓C交于
兩點．點
為橢圓上一點，求
的面積的最大值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
.
（1）當
時，求
的最小值
；
（2）是否存在實數
，
同時滿足下列條件：①
；②當的定義域為
時，其值域為
.若存在，求出，的值，若不存在，說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】甲、乙兩隊進行籃球決賽，采取五場三勝制（當一隊贏得三場勝利時，該隊獲勝，決賽結束）. 根據前期比賽成績，甲隊的主客場安排依次為“主主客客主”. 設甲隊主場取勝的概率為0.6，客場取勝的概率為0.5，且各場比賽結果相互獨立，則甲隊以3:1獲勝的概率為（ ）
A.0.15B.0.21C.0.24D.0.30
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
定義域為
，設
.
（1）試確定
的取值范圍，使得函數
在
上為單調函數；
（2）求證：
；
（3）求證：對于任意的
，總存在
，滿足
，并確定這樣的
的個數.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在全面抗擊新冠肺炎疫情這一特殊時期，我市教育局提出“停課不停學”的口號，鼓勵學生線上學習.某校數學教師為了調查高三學生數學成績與線上學習時間之間的相關關系，對高三年級隨機選取45名學生進行跟蹤問卷，其中每周線上學習數學時間不少于5小時的有19人，余下的人中，在檢測考試中數學平均成績不足120分的占
，統計成績后得到如下
列聯表：
分數不少于120分 | 分數不足120分 | 合計 | |
線上學習時間不少于5小時 | 4 | 19 | |
線上學習時間不足5小時 | |||
合計 | 45 |
（1）請完成上面列聯表；并判斷是否有99%的把握認為“高三學生的數學成績與學生線上學習時間有關”；
（2）在上述樣本中從分數不少于120分的學生中，按照分層抽樣的方法，抽到線上學習時間不少于5小時和線上學習時間不足5小時的學生共5名，若在這5名學生中隨機抽取2人，求至少1人每周線上學習時間不足5小時的概率.
（下面的臨界值表供參考）
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
（參考公式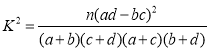
其中
）
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
