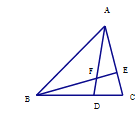
【題目】在
中，
分別是
上的點，
，
交于點
，若
，則四邊形
的面積為________。
【答案】
【解析】
連接DE，根據相似三角形的判定定理得出△DCE∽△ABC，進而判斷出AB∥CD、△DEF∽△ABF，再根據相似三角形的性質即可進行解答．
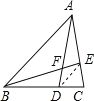連接DE，
∵AE=2CE，BD=2CD，
∴
=
，且夾角∠C為公共角，
∴△DCE∽△ABC，
∴∠CED=∠CAB，
∴AB∥DE，
∴△CDE∽△CBA，
∴
=
= 
，
∴
= 
，
∵S△ABC=3，
∴S△CDE=3×=，
且∠EDA=∠BAD，∠BED=∠ABE，
∴△DEF∽△ABF，
∴
==，
∴設S△DEF=x,則S△AEF=S△BDF=3x,S△ABF=9x，
∴x+3x+3x+9x=3，
解得：x=
，
∴S△DEF=，
∴S△DEF+S△CDE=+
=.
故答案為：
.
小學教材全測系列答案
小學數學口算題卡脫口而出系列答案科目：初中數學 來源： 題型：
【題目】如圖（1），P為△ABC所在平面上一點，且∠APB=∠BPC=∠CPA=120°，則點P叫做△ABC的費馬點．
（1）如果點P為銳角△ABC的費馬點，且∠ABC=60°．
①求證：△ABP∽△BCP；
②若PA=3，PC=4，則PB= ．
（2）已知銳角△ABC，分別以AB、AC為邊向外作正△ABE和正△ACD，CE和BD 相交于P點．如圖（2）
①求∠CPD的度數；
②求證：P點為△ABC的費馬點．
查看答案和解析>>
科目：初中數學 來源： 題型：
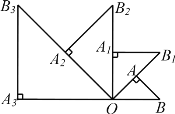
【題目】如圖，△ OAB 是腰長為 1 的等腰直角三角形， OAB 90°，延長OA 至 B1 ，使 AB1 OA ，以OB1 為底，在△ OAB 外側作等腰直角三角形OA1B1 ，再延長OA1 至 B2 ， 使 A1B2 OA1 ，以OB2 為底，在△ OA1B1 外側作等腰直角三角形OA2 B2 ，……，按此規律作等腰直角三角形OAn Bn （ n 1 ， n 為正整數），回答下列問題：
（1） A3B3 的長是_____________；（2）△ OA2020 B2020 的面積是_____________．
查看答案和解析>>
科目：初中數學 來源： 題型：
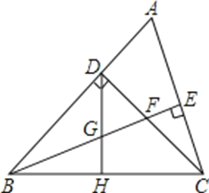
【題目】已知：如圖，△ABC中，∠ABC＝45°，CD⊥AB于D，BE平分∠ABC，且BE⊥AC于E，與CD相交于點F，H是BC邊的中點，連結DH與BE相交于點G．
（1）求證：BF＝AC；
（2）求證：CE＝
BF．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，已知點
在
的
邊上，
交
于
，
交
于
，若添加條件________，則四邊形
是矩形；若添加條件________，則四邊形是菱形；若添加條件________，則四邊形是正方形．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】商場某種商品平均每天可銷售30件，每件盈利50元。為了盡快減少庫存，商場決定采取適當的降價措施。經調查發現，每件商品每降價1元，商場平均每天可多售出2件。設每件商品降價
元。據此規律，請回答：
（1）商場日銷售量增加_____件，每件商品盈利_____元（用含
的代數式表示）。
（2）在上述條件不變、銷售正常情況下，每件商品降價多少元時，商場日盈利可達到2100元？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在平面直角坐標系中，將
繞點
順時針旋轉到
的位置，點
、
分別落在點
、
處，點在
軸上，再將繞點順時針旋轉到
的位置，點
在軸上，將繞點順時針旋轉到
的位置，點
在軸上，依次進行下去…．若點
，
，則點
的坐標為（ ）
A. 
B. 
C. 
D. 
科目：初中數學 來源： 題型：
【題目】小華和小峰是兩名自行車愛好者，小華的騎行速度比小峰快
兩人準備在周長為250米的賽道上進行一場比賽若小華在小峰出發15秒之后再出發，圖中
、
分別表示兩人騎行路程與時間的關系．
小峰的速度為______米
秒，他出發______米后，小華才出發；
小華為了能和小峰同時到達終點，設計了兩個方案，方案一：加快騎行速度；方案二：比預定時間提前出發．
圖______
填“A“”或“B“
代表方案一；
若采用方案二，小華必須在小峰出發多久后開始騎行？求出此時小華騎行的路程與時間的函數關系式．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在等邊△ABC中，DE分別是邊AB、AC上的點，且AD＝CE，則∠ADC+∠BEA＝（ ）
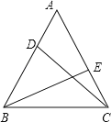
A.180°B.170°C.160°D.150°
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com