
【題目】小華和小峰是兩名自行車愛好者,小華的騎行速度比小峰快![]() 兩人準備在周長為250米的賽道上進行一場比賽
兩人準備在周長為250米的賽道上進行一場比賽![]() 若小華在小峰出發15秒之后再出發,圖中
若小華在小峰出發15秒之后再出發,圖中![]() 、
、![]() 分別表示兩人騎行路程與時間的關系.
分別表示兩人騎行路程與時間的關系.
![]() 小峰的速度為______米
小峰的速度為______米![]() 秒,他出發______米后,小華才出發;
秒,他出發______米后,小華才出發;
![]() 小華為了能和小峰同時到達終點,設計了兩個方案,方案一:加快騎行速度;方案二:比預定時間提前出發.
小華為了能和小峰同時到達終點,設計了兩個方案,方案一:加快騎行速度;方案二:比預定時間提前出發.
![]() 圖______
圖______![]() 填“A“”或“B“
填“A“”或“B“![]() 代表方案一;
代表方案一;
![]() 若采用方案二,小華必須在小峰出發多久后開始騎行?求出此時小華騎行的路程與時間的函數關系式.
若采用方案二,小華必須在小峰出發多久后開始騎行?求出此時小華騎行的路程與時間的函數關系式.

【答案】(1)5;75;(2)①B;②小華必須在小峰出發![]() 秒后開始騎行;
秒后開始騎行;![]() .
.
【解析】
![]() 根據圖象解答即可;
根據圖象解答即可;
![]() 由圖象可知,圖B表示加快騎行速度;
由圖象可知,圖B表示加快騎行速度;![]() 求出小華騎行的速度即可求出小華騎行的時間,從而求出小華必須在小峰出發后開始騎行時間;再用待定系數法解答即可求出此時小華騎行的路程與時間的函數關系式.
求出小華騎行的速度即可求出小華騎行的時間,從而求出小華必須在小峰出發后開始騎行時間;再用待定系數法解答即可求出此時小華騎行的路程與時間的函數關系式.
![]() 小峰的速度為:
小峰的速度為:![]() 米
米![]() 秒
秒![]() ,他出發
,他出發![]() 米
米![]() 后,小華才出發.
后,小華才出發.
故答案為:5;75.
![]() 由圖象可知,圖B表示加快騎行速度,
由圖象可知,圖B表示加快騎行速度,
故答案為:B;
![]() 小華騎行的速度為
小華騎行的速度為![]() 米
米![]() 秒
秒![]() ,
,
小華騎行的時間為:![]() 秒
秒![]() ,
,
![]() 秒
秒![]() ,
,
即小華必須在小峰出發![]() 秒后開始騎行;
秒后開始騎行;
設此時小華騎行的路程與時間的函數關系式為![]() ,根據題意得,
,根據題意得,
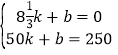 ,解得
,解得![]() ,
,
所以此時小華騎行的路程與時間的函數關系式為![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】二次函數 ![]() (
( ![]() )的圖像如圖所示,下列結論:①
)的圖像如圖所示,下列結論:① ![]() ;②當
;②當 ![]() 時,y隨x的增大而減小;③
時,y隨x的增大而減小;③ ![]() ;④
;④ ![]() ;⑤
;⑤ ![]() ,其中正確的個數是( )
,其中正確的個數是( )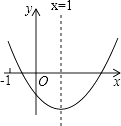
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在邊長為2的等邊△ABC中,D是BC的中點,點E在線段AD上,連結BE,在BE的下方作等邊△BEF,連結DF.當△BDF的周長最小時,∠DBF的度數是_____.
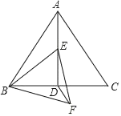
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖, ![]() 的圖像交x軸于O點和A點,將此拋物線繞原點旋轉180°得圖像y2 , y2與x軸交于O點和B點.
的圖像交x軸于O點和A點,將此拋物線繞原點旋轉180°得圖像y2 , y2與x軸交于O點和B點.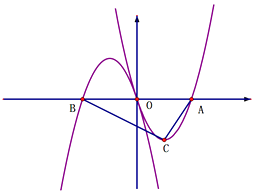
(1)若y1=2x2-3x,則y2= .
(2)設 y 1 的頂點為C,則當△ABC為直角三角形時,請你任寫一個符合此條件的 y 1 的表達式 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】平面直角坐標系 ![]() 中,
中, ![]() 是坐標原點。已知A(0,
是坐標原點。已知A(0, ![]() ),B(1,0),C(6,
),B(1,0),C(6, ![]() ),有一拋物線恰好經過這三點.
),有一拋物線恰好經過這三點.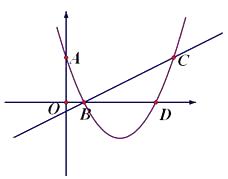
(1)求該拋物線解析式;
(2)若拋物線交 ![]() 軸的另一交點為D,那么拋物線上是否存在一點P,使得
軸的另一交點為D,那么拋物線上是否存在一點P,使得 ![]() ,若存在,求出P的坐標,若不存在,請說明理由。
,若存在,求出P的坐標,若不存在,請說明理由。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,四邊形ABCD 是⊙O的內接四邊形,∠ABC=2∠D,連接OA,OC,AC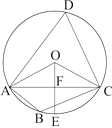
(1)求∠OCA的度數
(2)如果OE ![]() AC于F,且OC=
AC于F,且OC= ![]() , 求AC的長
, 求AC的長
查看答案和解析>>
科目:初中數學 來源: 題型:
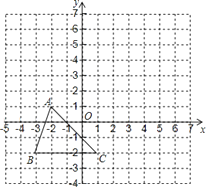
【題目】如圖,在平面直角坐標系網格中,△ABC的頂點都在格點上,點C坐標(0,-1).
(1)①作出△ABC 關于原點對稱的△A1B1C1 , 并寫出點A1的坐標;
②把△ABC 繞點C逆時針旋轉90°,得△A2B2C2 , 畫出△A2B2C2 , 并寫出點A2的坐標;
(2)直接寫出△A2B2C2的面積
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:如圖,把△ABC向上平移3個單位長度,再向右平移2個單位長度,得到△A![]() B
B![]() C
C![]() .
.
(1)在圖中畫出△A![]() B
B![]() C
C![]() ;
;
(2)寫出點A![]() 、B
、B![]() 、C
、C![]() 的坐標;
的坐標;
(3)在![]() 軸上是否存在一點P,使得△PBC與△ABC面積相等?若存在,寫出點P的坐標;若不存在,說明理由.
軸上是否存在一點P,使得△PBC與△ABC面積相等?若存在,寫出點P的坐標;若不存在,說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com