【題目】二次函數 
（ 
）的圖像如圖所示，下列結論：① 
；②當 
時，y隨x的增大而減小；③ 
；④ 
；⑤ 
，其中正確的個數是（ ）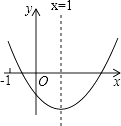
A.1
B.2
C.3
D.4
【答案】B
【解析】①由圖像可知：拋物線開口向上，與y軸負半軸相交，
∴a
0，c
0，
∴ac0.
∴①錯誤.
②由圖像可知：拋物線開口向上，對稱軸x=1，
∴當 x ≥ 1 時，y隨x的增大而增大；
∴②錯誤.
③由圖像可知：對稱軸x=-
=1，
∴2a+b=0.
∴③正確.
④由圖像可知：拋物線與x軸有兩個交點，
∴b2-4ac0.
∴④錯誤.
⑤由圖像可知：當x=-1時y0，再由函數性質知當 x 
1 時，y隨x的增大而減少；
∴當x=-2時，4a-2b+c0.
∴⑤正確.
所以答案是：B.
【考點精析】根據題目的已知條件，利用二次函數的性質和二次函數圖象以及系數a、b、c的關系的相關知識可以得到問題的答案，需要掌握增減性：當a>0時，對稱軸左邊，y隨x增大而減小；對稱軸右邊，y隨x增大而增大；當a<0時，對稱軸左邊，y隨x增大而增大；對稱軸右邊，y隨x增大而減小；二次函數y=ax2+bx+c中，a、b、c的含義：a表示開口方向：a>0時，拋物線開口向上; a<0時，拋物線開口向下b與對稱軸有關：對稱軸為x=-b/2a;c表示拋物線與y軸的交點坐標：（0，c）．
考前必練系列答案科目：初中數學 來源： 題型：
【題目】△ABC在平面直角坐標系中的位置如圖所示．
（1）在圖中畫出△ABC與關于y軸對稱的圖形△A1B1C1，并寫出頂點A1、B1、C1的坐標；
（2）若將線段A1C1平移后得到線段A2C2，且A2（a，2），C2（-2，b），求a+b的值．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖,已知A(3，0),B(0，-1)，連接AB,過B點作AB的垂線段,使BA=BC,連接AC.
(1)如圖1，求C點坐標；
(2)如圖2,若P點從A點出發,沿x軸向左平移,連接BP,作等腰直角三角形△BPQ,連接CQ.求證:PA=CQ.
(3)在(2)的條件下,若C、P、Q三點共線,求此時P點坐標及∠APB的度數.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】觀察下列式子：
0×2+1＝12……①
1×3+1＝22……②
2×4+1＝32……③
3×5+1＝42……④
……
（1）第⑤個式子 ，第⑩個式子 ；
（2）請用含n（n為正整數）的式子表示上述的規律，并證明：
（3）求值：（1+
）（1+
）（1+
）（1+
）…（1+
）．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某中學學生步行到郊外旅行，七年級
班學生組成前隊，步行速度為4千米
小時，七
班的學生組成后隊，速度為6千米小時；前隊出發1小時后，后隊才出發，同時后隊派一名聯絡員騎自行車在兩隊之間不間斷地來回聯絡，他騎車的速度為10千米小時．
后隊追上前隊需要多長時間？
后隊追上前隊的時間內，聯絡員走的路程是多少？
七年級班出發多少小時后兩隊相距2千米？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】小華和小峰是兩名自行車愛好者，小華的騎行速度比小峰快
兩人準備在周長為250米的賽道上進行一場比賽若小華在小峰出發15秒之后再出發，圖中
、
分別表示兩人騎行路程與時間的關系．
小峰的速度為______米
秒，他出發______米后，小華才出發；
小華為了能和小峰同時到達終點，設計了兩個方案，方案一：加快騎行速度；方案二：比預定時間提前出發．
圖______
填“A“”或“B“
代表方案一；
若采用方案二，小華必須在小峰出發多久后開始騎行？求出此時小華騎行的路程與時間的函數關系式．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在△ABC中，∠BAC=60°，∠BAC的平分線AD與邊BC的垂直平分線MD相交于點D，DE⊥AB交AB的延長線于點E，DF⊥AC于點F，現有下列結論：①DE=DF；②DE+DF=AD；③DM平分∠ADF；④AB+AC=2AE.其中，正確的有（ ）
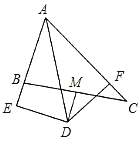
A. 1個 B. 2個 C. 3個 D. 4個
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
