
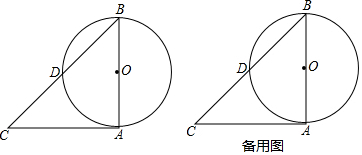
分析 (1)先連接AD,CO,交于點F,則點F為△ABC的重心,連接BF并延長,交AC于E,則E是AC的中點,BE是△ABC的中線;
(2)過點D,E作直線DT,連接OD,則直線DT即為所求.
解答 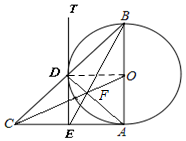 解:(1)如圖所示,∵AB是⊙O的直徑,AC是⊙O的切線,
解:(1)如圖所示,∵AB是⊙O的直徑,AC是⊙O的切線,
∴AC⊥AB,
又∵AC=AB,
∴△ABC是等腰直角三角形,
連接AD,CO,交于點F,則AD⊥BC,
∴點D是BC的中點,
又∵O是AB的中點,
∴點F是△ABC的重心,
連接BF并延長,交AC于E,則E是AC的中點,
∴BE是△ABC的中線;
(2)如圖所示,過點D,E作直線DT,連接OD,則直線DT即為所求.
由(1)可得,△ABD、△ACD都是等腰直角三角形,
∴OD⊥AB,DE⊥AC,
又∵AB⊥AC,
∴∠ODE=90°,
∴DE是⊙O的切線.
點評 本題主要考查了切線的性質以及三角形重心的運用,解決問題的關鍵是掌握:圓的切線垂直于經過切點的半徑.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案 目標測試系列答案
目標測試系列答案科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 (1)有理數a,b在數軸上位置如圖所示,求-|a|+|b|;
(1)有理數a,b在數軸上位置如圖所示,求-|a|+|b|;查看答案和解析>>
科目:初中數學 來源: 題型:解答題
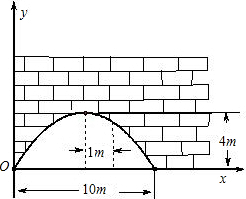 有一個拋物線形的拱形橋洞,橋洞離水面的最大高度為 4m,跨度為 10m,如圖所示,把它的圖形放在直角坐標系中.
有一個拋物線形的拱形橋洞,橋洞離水面的最大高度為 4m,跨度為 10m,如圖所示,把它的圖形放在直角坐標系中.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
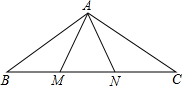 如圖,△ABN≌△ACM,AB=AC,BN=CM,∠B=50°,∠ANB=60°,則∠MAC的度數等于( )
如圖,△ABN≌△ACM,AB=AC,BN=CM,∠B=50°,∠ANB=60°,則∠MAC的度數等于( )| A. | 120° | B. | 70° | C. | 60° | D. | 50°. |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com