
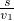 =
=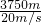 =187.5秒
=187.5秒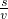 =
= =250s,
=250s,

科目:初中物理 來源: 題型:
查看答案和解析>>
科目:初中物理 來源:湖北省黃岡地區2012屆九年級四科聯賽物理試題(A卷) 題型:038
相距3750 m的甲、乙兩車站之間有一條筆直的公路,每隔2 min有一輛摩托車由甲站出發以20 m/s的速度勻速開往乙站,每一輛摩托車在抵達乙站后都立即掉頭以10 m/s的速度勻速開回甲站.這樣往返的車輛共有48輛;若在第一輛摩托車開出的同時,有一輛汽車由甲站出發勻速開始乙站,速度為15 m/s,問汽車抵達乙站前最后將與從甲站開出的第幾輛摩托車迎面相遇?相遇處距乙站多少米?
查看答案和解析>>
科目:初中物理 來源:不詳 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com