已知數列{an}的前n項的和為Sn,且Sn=2n+7-2an.
(1)求證:{an-2}為等比數列;
(2)是否存在實數k,使得an≤n3+kn2+9n對于任意的n∈N*都成立,若存在,求出實數k的取值范圍;若不存在,說明理由.
解:(1)n=1時,a
1=S
1=2+7-2a
1,解得a
1=3.
n≥2時,a
n=S
n-S
n-1=2-2a
n+2a
n-1,
即3a
n=2a
n-1+2,
∴
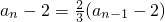
,
∴{a
n-2}是首項為1,公比為

的等比數列.
(2)由(1)知
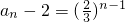
,
∴
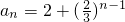
,
由2+(

)
n-1≤n
3+kn
2+9n,
得

.
∴只需求出

的最大值即可.
設
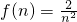
,
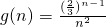
,
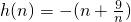
,
∵n∈N
*,∴f(n)單調遞減.
∵
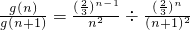
=
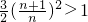
,
∴g(n)<g(n+1),
故g(n)單調遞減.
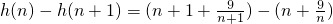
=
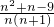
,
當n≥3時,h(n)>h(n+1),
故n≥3時,h(n)單調遞減.
∴n≥3時,

隨著n的增大而減小,
∵p(1)=-7,
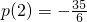
,
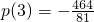
,
∴p(n)的最大值為p(3)=-
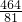
.
故k≥
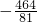
.
分析:(1)由n=1,解得a
1=3.由n≥2,得3a
n=2a
n-1+2,故
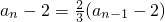
,由此能夠證明{a
n-2}是首項為1,公比為

的等比數列.
(2)由
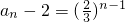
,知
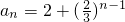
,由2+(

)
n-1≤n
3+kn
2+9n,得

.故只需求出

的最大值即可得到k范圍.
點評:本題考查等比數列的證明和數列與不等式的綜合運用,考查運算求解能力,推理論證能力;考查化歸與轉化思想.對數學思維的要求比較高,有一定的探索性.綜合性強,難度大,是高考的重點,易錯點是判斷最大值時因解題能力差導致失誤.解題時要認真審題,仔細解答,注意提高解題能力.

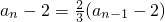 ,
, 的等比數列.
的等比數列.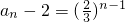 ,
,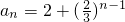 ,
, )n-1≤n3+kn2+9n,
)n-1≤n3+kn2+9n, .
. 的最大值即可.
的最大值即可.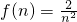 ,
,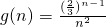 ,
,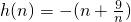 ,
,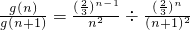
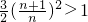 ,
,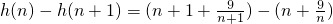 =
=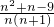 ,
, 隨著n的增大而減小,
隨著n的增大而減小,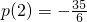 ,
,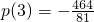 ,
,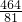 .
.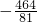 .
.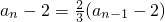 ,由此能夠證明{an-2}是首項為1,公比為
,由此能夠證明{an-2}是首項為1,公比為 的等比數列.
的等比數列.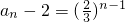 ,知
,知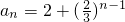 ,由2+(
,由2+( )n-1≤n3+kn2+9n,得
)n-1≤n3+kn2+9n,得 .故只需求出
.故只需求出 的最大值即可得到k范圍.
的最大值即可得到k范圍.
