日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

【題目】將一個正方形紙片放置在平面直角坐標系中，點，點，，點．動點在邊上，點在邊上，沿折疊該紙片，使點的對應點始終落在邊上（點不與重合），點落在點處，與交于點．

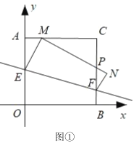
（Ⅰ）如圖①，當時，求點的坐標；

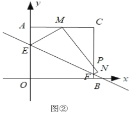
（Ⅱ）如圖②，當點落在的中點時，求點的坐標；

（Ⅲ）隨著點在邊上位置的變化，的周長是否發生變化？如變化，簡述理由；如不變，直接寫出其值．

【題目】甲、乙兩個批發店銷售同一種蘋果，在甲批發店，不論一次購買數量是多少，價格均為6元/．在乙批發店，一次購買數量不超過時，價格為7元/；一次購買數量超過時，其中有的價格仍為7元/，超過部分的價格為5元/．設小王在同一個批發店一次購買蘋果的數量為．

（Ⅰ）根據題意填空：

①若一次購買數量為時，在甲批發店的花費為________元，在乙批發店的花費為________元；

②若一次購買數量為時，在甲批發店的花費為________元，在乙批發店的花費為________元；

（Ⅱ）設在甲批發店花費元，在乙批發店花費元，分別求，關于的函數解析式；

（Ⅲ）根據題意填空：

①若小王在甲批發店和在乙批發店一次購買蘋果的數量相同，且花費相同，則他在同一個批發店一次購買蘋果的數量為_________；

②若小王在同一個批發店一次購買蘋果的數量為，則他在甲、乙兩個批發店中的________批發店購買花費少；

③若小王在同一個批發店一次購買蘋果花費了260元，則他在甲、乙兩個批發店中的_________批發店購買數量多．

【題目】如圖，是的直徑，是的弦，過點的切線交延長線于點．

（Ⅰ）若，求的度數；

（Ⅱ）若，求的長．

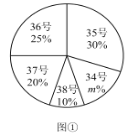
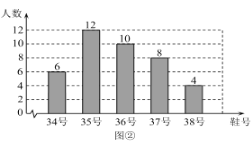
（Ⅰ）本次接受隨機抽樣調查的學生人數為________，圖①中的值為________；

（Ⅱ）求本次調查獲取的樣本數據的眾數和中位數；

（Ⅲ）根據樣本數據，若學校計劃購買150雙運動鞋,建議購買35號運動鞋多少雙？

【題目】已知拋物線與直線有兩個不同的交點．下列結論：①；②當時，有最小值；③方程有兩個不等實根；④若連接這兩個交點與拋物線的頂點，恰好是一個等腰直角三角形，則；其中正確的結論的個數是（ ）

A.4B.3C.2D.1

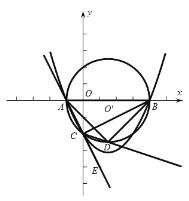
【題目】已知：二次函數的圖象與軸交于兩點，其中點，與軸負半軸交于點，起對稱軸是直線．

（1）求二次函數的解析式；

（2）圓經過點的外接圓，點是延長線上一點，的平分線交圓于點，連接、，求的面積；

（3）在（2）的條件下，二次函數的圖象上是否存在點，使得？如果存在，請求出所有符合條件的點坐標；如果不存在，請說明理由．

【題目】有一邊是另一邊的倍的三角形叫做智慧三角形，這兩邊中較長邊稱為智慧邊，這兩邊的夾角叫做智慧角．

（1）已知為智慧三角形，且的一邊長為，則該智慧三角形的面積為_________；

（2）如圖①，在中，，，求證：是智慧三角形；

（3）如圖②，是智慧三角形，為智慧邊，為智慧角，，點在函數（）的圖象上，點在點的上方，且點的縱坐標為，當是直角三角形時，求的值．

【題目】公歷3月12日是植樹節，為宣傳保護數目，激發人們愛林造林的熱情，政府投資13萬元給某村民小組用于購買與種植兩種樹苗共3000棵，完成這項種植后，剩余的款項作為村民小組的純收入，已知用160元購買樹苗比購買樹苗多3棵，這兩種樹苗的單價、成活率及移栽費用見下表：

（1）求表中的值；

（2）設購買樹苗棵，其它購買的是樹苗，把這些樹苗種植完成后，村民小組獲得的純收入為元，請你寫出與之間的函數關系式；

（3）若要求這批樹苗種植后，成活率達到93%以上（包含93%），則最多種植樹苗多少棵？此時，村民小組在這項工作中，所得的純收入最大值可以是多少元？

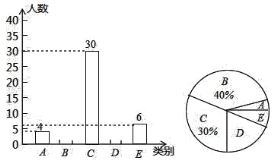
【題目】為規范學生的在校表現，我校某班實行了操行評分制，根據學生的操行分高低分為五個等級，現對該班本學期的操行等級進行了統計，并繪制了不完整的兩種統計圖，請根據圖象回答問題：

（1）類所對應的圓心角是_________度，樣本中成績的中位數落在_________類中，并補全條形統計圖；

（2）若類含有2名男生和2名女生，隨機選擇2名學生參加下學期開學的“國旗下的講話”演講活動，請用列表法或畫樹狀圖法求恰好抽到1名男生和1名女生的概率．

【題目】若平面直角坐標系內的點滿足橫、縱坐標都為整數，則把點叫做 “整點”．例如：、都是“整點”，拋物線（）與軸交于兩點，若該拋物線在之間的部分與線段所圍成的區域（包括邊界）恰有七個整點，則的取值范圍是（　　）

A.B.

C.D.