
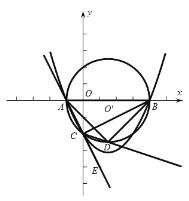
【題目】已知:二次函數![]() 的圖象與
的圖象與![]() 軸交于
軸交于![]() 兩點,其中點
兩點,其中點![]() ,與
,與![]() 軸負半軸交于點
軸負半軸交于點![]() ,起對稱軸是直線
,起對稱軸是直線![]() .
.
(1)求二次函數![]() 的解析式;
的解析式;
(2)圓![]() 經過點
經過點![]() 的外接圓,點
的外接圓,點![]() 是
是![]() 延長線上一點,
延長線上一點,![]() 的平分線交圓
的平分線交圓![]() 于點
于點![]() ,連接
,連接![]() 、
、![]() ,求
,求![]() 的面積;
的面積;
(3)在(2)的條件下,二次函數![]() 的圖象上是否存在點
的圖象上是否存在點![]() ,使得
,使得![]() ?如果存在,請求出所有符合條件的
?如果存在,請求出所有符合條件的![]() 點坐標;如果不存在,請說明理由.
點坐標;如果不存在,請說明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)存在,
;(3)存在,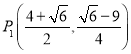 ,
,
【解析】
(1)根據拋物線的對稱性,可以求出點B的坐標,再用待定系數法求解即可;
(2)根據![]() 以及圓的相關性質,可知△ABD為等腰直角三角形,從而得出
以及圓的相關性質,可知△ABD為等腰直角三角形,從而得出![]() 與
與![]() 的數量關系,列式求解即可;
的數量關系,列式求解即可;
(3)使得![]() 的點存在兩種情況,利用相似導出線段之間的比值,再用直線和拋物線的解析式聯立求得相關點的坐標.
的點存在兩種情況,利用相似導出線段之間的比值,再用直線和拋物線的解析式聯立求得相關點的坐標.
(1)∵點![]() ,對稱軸為
,對稱軸為![]()
∴![]()
將![]() 、
、![]() 、
、![]() 代入
代入![]() 中
中
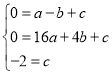
解得![]()
∴拋物線的解析式為:![]()
(2)∵![]() ,
,![]() ,
,![]()
∴![]() ,
,![]() ,
,![]() ,
,
∴![]()
又∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]()
∴![]() 為圓
為圓![]() 的直徑,
的直徑,![]() 點坐標為
點坐標為![]() ,
,
∴![]()
又∵![]() 平分
平分![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() 為等腰直角三角形.
為等腰直角三角形.
連接![]() ,則
,則![]() ,
,![]() ,
,
∴![]() ,
,![]() 點坐標為
點坐標為![]()
設![]() 與
與![]() 軸交于點
軸交于點![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]()
作![]() 軸于點
軸于點![]() ,
,
∵![]() ,
,
∴![]() ,
,![]()
∴![]() ;
;
(3)拋物線上存在點![]() ,使得
,使得![]() .分兩種情況討論:
.分兩種情況討論:

①過點![]() 作直線
作直線![]() ,交
,交![]() 軸于
軸于![]() .
.
∵![]() ,
,
∴![]() ,
,![]()
又∵![]() ,
,
∴![]() ,直線
,直線![]() 與拋物線在
與拋物線在![]() 點右側的交點即為點
點右側的交點即為點![]() .
.
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]()
∵![]()
∴![]() ,
,![]() .
.
設直線![]() 的解析式為
的解析式為![]()
則有,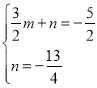
解得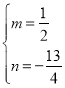 ,
,
直線![]() 的解析式為
的解析式為![]()
∴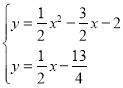
解得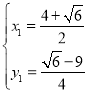 ,
,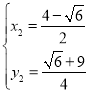 (舍)
(舍)
∴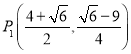
②過點![]() 作
作![]() ,交
,交![]() 軸于
軸于![]() 點.
點.
∵![]() ,
,
∴![]()
即直線![]() 與拋物線在
與拋物線在![]() 點右側的交點即為
點右側的交點即為![]() 點
點
又∵![]() ,
,
∴![]()
∴![]()
∴![]()
∴![]()
設直線![]() 的解析式為
的解析式為![]()
則有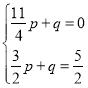 ,解得
,解得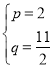 ,
,
∴直線![]() 的解析式為
的解析式為![]()
∴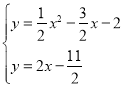 ,解得
,解得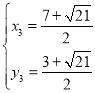 ,
,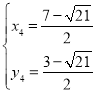 (舍)
(舍)
∴
∴符合條件的![]() 點有兩個:
點有兩個: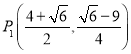 ,
, .
.


科目:初中數學 來源: 題型:
【題目】“精準扶貧”這是新時期黨和國家扶貧工作的精髓和亮點.某校團委隨機抽取部分學生,對他們是否了解關于“精準扶貧”的情況進行調查,調查結果有三種:A、了解很多;B、了解一點;C、不了解.團委根據調查的數據進行整理,繪制了尚不完整的統計圖如下,圖1中C區域的圓心角為36°,請根據統計圖中的相關的信息,解答下列問題:
(1)求本次活動共調查了 名學生;圖1中,B區域的圓心角度是 ;在抽取的學生中調查結果的中位數落在 區域里.
(2)補全條形統計圖.
(3)若該校有1200名學生,請估算該校不是了解很多的學生人數.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我們規定,以二次函數y=ax2+bx+c的二次項系數a的2倍為一次項系數,一次項系數b為常數項構造的一次函數y=2ax+b叫做二次函數y=ax2+bx+c的“子函數”,反過來,二次函數y=ax2+bx+c叫做一次函數y=2ax+b的“母函數”.
(1)若一次函數y=2x-4是二次函數y=ax2+bx+c的“子函數”,且二次函數經過點(3,0),求此二次函數的解析式及頂點坐標.
(2)若“子函數”y=x-6的“母函數”的最小值為1,求“母函數”的函數表達式.
(3)已知二次函數y=-x2-4x+8的“子函數”圖象直線l與x軸、y軸交于C、D兩點,動點P為二次函數y=-x2-4x+8對稱軸右側上的動點,求△PCD的面積的最大值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】二次函數![]() 的圖象如圖所示,有下列結論:①
的圖象如圖所示,有下列結論:①![]() ;②
;②![]() ;③若
;③若![]() 為任意實數,則
為任意實數,則![]() ;④a-b+c>0;⑤若
;④a-b+c>0;⑤若![]() ,且
,且![]() ,則
,則![]() .其中,正確結論的個數為( )
.其中,正確結論的個數為( )
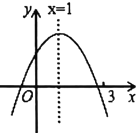
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中,![]() 為原點,拋物線
為原點,拋物線![]() 經過點
經過點![]() ,對稱軸為直線
,對稱軸為直線![]() ,點
,點![]() 關于直線
關于直線![]() 的對稱點為點
的對稱點為點![]() .過點
.過點![]() 作直線
作直線![]() 軸,交
軸,交![]() 軸于點
軸于點![]() .
.
(Ⅰ)求該拋物線的解析式及對稱軸;
(Ⅱ)點![]() 在
在![]() 軸上,當
軸上,當![]() 的值最小時,求點
的值最小時,求點![]() 的坐標;
的坐標;
(Ⅲ)拋物線上是否存在點![]() ,使得
,使得![]() ,若存在,求出點
,若存在,求出點![]() 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】將一個正方形紙片![]() 放置在平面直角坐標系中,點
放置在平面直角坐標系中,點![]() ,點
,點![]() ,
,![]() ,
,![]() 點.動點
點.動點![]() 在邊
在邊![]() 上,點
上,點![]() 在邊
在邊![]() 上,沿
上,沿![]() 折疊該紙片,使點
折疊該紙片,使點![]() 的對應點
的對應點![]() 始終落在邊
始終落在邊![]() 上(點
上(點![]() 不與
不與![]() 重合),點
重合),點![]() 落在點
落在點![]() 處,
處,![]() 與
與![]() 交于點
交于點![]() .
.
(Ⅰ)如圖①,當![]() 時,求點
時,求點![]() 的坐標;
的坐標;
(Ⅱ)如圖②,當點![]() 落在
落在![]() 的中點時,求點
的中點時,求點![]() 的坐標;
的坐標;
(Ⅲ)隨著點![]() 在
在![]() 邊上位置的變化,
邊上位置的變化,![]() 的周長是否發生變化?如變化,簡述理由;如不變,直接寫出其值.
的周長是否發生變化?如變化,簡述理由;如不變,直接寫出其值.
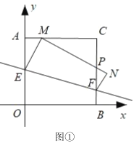
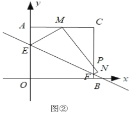
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,二次函數![]() (其中
(其中![]() )的圖象與x軸分別交于點A、B(點A位于B的左側),與y軸交于點C,過點C作x軸的平行線CD交二次函數圖像于點D.
)的圖象與x軸分別交于點A、B(點A位于B的左側),與y軸交于點C,過點C作x軸的平行線CD交二次函數圖像于點D.
(1)當m2時,求A、B兩點的坐標;
(2)過點A作射線AE交二次函數的圖像于點E,使得BAEDAB.求點E的坐標(用含m的式子表示);
(3)在第(2)問的條件下,二次函數![]() 的頂點為F,過點C、F作直線與x軸于點G,試求出GF、AD、AE的長度為三邊長的三角形的面積(用含m的式子表示).
的頂點為F,過點C、F作直線與x軸于點G,試求出GF、AD、AE的長度為三邊長的三角形的面積(用含m的式子表示).
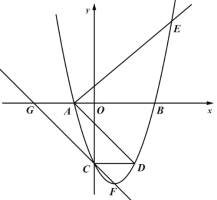
查看答案和解析>>
科目:初中數學 來源: 題型:
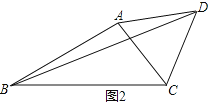
【題目】已知△ABC,以AC為邊在△ABC外作等腰△ACD,其中AC=AD
(1) 如圖1,若AB為邊在△ABC外作△ABE,AB=AE,∠DAC=∠EAB=60°,求∠BFC的度數
(2) 如圖2,∠ABC=α,∠ACD=β,BC=6,BD=8
① 若α=30°,β=60°,AB的長為
② 若改變α、β的大小,但α+β=90°,求△ABC的面積
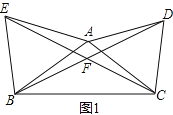
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了落實黨的“精準扶貧”政策,A、B兩城決定向C、D兩鄉運送肥料以支持農村生產,已知A、B兩城共有肥料500噸,其中A城肥料比B城少100噸,從A城往C、D兩鄉運肥料的費用分別為20元/噸和25元/噸;從B城往C、D兩鄉運肥料的費用分別為15元/噸和24元/噸.現C鄉需要肥料240噸,D鄉需要肥料260噸.
(1)A城和B城各有多少噸肥料?
(2)設從A城運往C鄉肥料x噸,總運費為y元,求出最少總運費.
(3)由于更換車型,使A城運往C鄉的運費每噸減少a(0<a<6)元,這時怎樣調運才能使總運費最少?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com