相關習題
0 151475 151483 151489 151493 151499 151501 151505 151511 151513 151519 151525 151529 151531 151535 151541 151543 151549 151553 151555 151559 151561 151565 151567 151569 151570 151571 151573 151574 151575 151577 151579 151583 151585 151589 151591 151595 151601 151603 151609 151613 151615 151619 151625 151631 151633 151639 151643 151645 151651 151655 151661 151669 366461
科目:
來源:2013年江蘇省連云港市中考數學試卷(解析版)
題型:解答題
計算(

)
-1+(
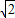
-1)
+2×(-3)
查看答案和解析>>
科目:
來源:2013年江蘇省連云港市中考數學試卷(解析版)
題型:解答題
解不等式組
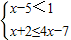
.
查看答案和解析>>
科目:
來源:2013年江蘇省連云港市中考數學試卷(解析版)
題型:解答題
查看答案和解析>>
科目:
來源:2013年江蘇省連云港市中考數學試卷(解析版)
題型:解答題
某校為了解“理化生實驗操作”考試的備考情況,隨機抽取了一部分九年級學生進行測試,測試結果分為“優秀”、“良好”、“合格”、“不合格”四個等級,分別記為A、B、C、D.根據測試結果繪制了如下尚不完整的統計圖.
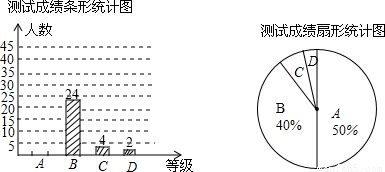
(1)本次測試共隨機抽取了______名學生.請根據數據信息補全條形統計圖;
(2)若該校九年級的600名學生全部參加本次測試,請估計測試成績等級在合格以上(包括合格)的學生約有多少人?
查看答案和解析>>
科目:
來源:2013年江蘇省連云港市中考數學試卷(解析版)
題型:解答題
甲、乙、丙三人之間相互傳球,球從一個人手中隨機傳到另外一個人手中,共傳球三次.
(1)若開始時球在甲手中,求經過三次傳球后,球傳回到甲手中的概率是多少?
(2)若乙想使球經過三次傳遞后,球落在自己手中的概率最大,乙會讓球開始時在誰手中?請說明理由.
查看答案和解析>>
科目:
來源:2013年江蘇省連云港市中考數學試卷(解析版)
題型:解答題
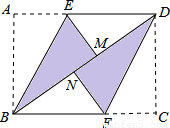
在矩形ABCD中,將點A翻折到對角線BD上的點M處,折痕BE交AD于點E.將點C翻折到對角線BD上的點N處,折痕DF交BC于點F.
(1)求證:四邊形BFDE為平行四邊形;
(2)若四邊形BFDE為菱形,且AB=2,求BC的長.
查看答案和解析>>
科目:
來源:2013年江蘇省連云港市中考數學試卷(解析版)
題型:解答題
小林準備進行如下操作實驗;把一根長為40cm的鐵絲剪成兩段,并把每一段各圍成一個正方形.
(1)要使這兩個正方形的面積之和等于58cm2,小林該怎么剪?
(2)小峰對小林說:“這兩個正方形的面積之和不可能等于48cm2.”他的說法對嗎?請說明理由.
查看答案和解析>>
科目:
來源:2013年江蘇省連云港市中考數學試卷(解析版)
題型:解答題
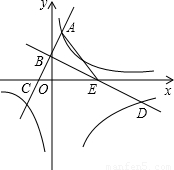
如圖,已知一次函數y=2x+2的圖象與y軸交于點B,與反比例函數y=

的圖象的一個交點為A(1,m).過點B作AB的垂線BD,與反比例函數y=
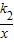
(x>0)的圖象交于點D(n,-2).
(1)求k
1和k
2的值;
(2)若直線AB、BD分別交x軸于點C、E,試問在y軸上是否存在一個點F,使得△BDF∽△ACE?若存在,求出點F的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:
來源:2013年江蘇省連云港市中考數學試卷(解析版)
題型:解答題
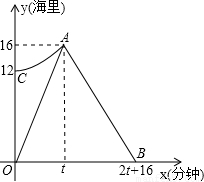
我市某海域內有一艘輪船發生故障,海事救援船接到求救信號后立即從港口出發沿直線勻速前往救援,與故障漁船會合后立即將其拖回.如圖折線段O-A-B表示救援船在整個航行過程中離港口的距離y(海里)隨航行時間x(分鐘)的變化規律.拋物線y=ax
2+k表示故障漁船在漂移過程中離港口的距離y(海里)隨漂移時間x(分鐘)的變化規律.已知救援船返程速度是前往速度的

.根據圖象提供的信息,解答下列問題:
(1)救援船行駛了______海里與故障船會合;
(2)求該救援船的前往速度;
(3)若該故障漁船在發出求救信號后40分鐘內得不到營救就會有危險,請問救援船的前往速度每小時至少是多少海里,才能保證故障漁船的安全.
查看答案和解析>>
科目:
來源:2013年江蘇省連云港市中考數學試卷(解析版)
題型:解答題
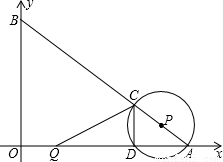
如圖,在平面直角坐標系中,O為坐標原點,點A、B的坐標分別為(8,0)、(0,6).動點Q從點O、動點P從點A同時出發,分別沿著OA方向、AB方向均以1個單位長度/秒的速度勻速運動,運動時間為t(秒)(0<t≤5).以P為圓心,PA長為半徑的⊙P與AB、OA的另一個交點分別為C、D,連接CD、QC.
(1)求當t為何值時,點Q與點D重合?
(2)設△QCD的面積為S,試求S與t之間的函數關系式,并求S的最大值;
(3)若⊙P與線段QC只有一個交點,請直接寫出t的取值范圍.
查看答案和解析>>


 在矩形ABCD中,將點A翻折到對角線BD上的點M處,折痕BE交AD于點E.將點C翻折到對角線BD上的點N處,折痕DF交BC于點F.
在矩形ABCD中,將點A翻折到對角線BD上的點M處,折痕BE交AD于點E.將點C翻折到對角線BD上的點N處,折痕DF交BC于點F. 如圖,已知一次函數y=2x+2的圖象與y軸交于點B,與反比例函數y=
如圖,已知一次函數y=2x+2的圖象與y軸交于點B,與反比例函數y= 的圖象的一個交點為A(1,m).過點B作AB的垂線BD,與反比例函數y=
的圖象的一個交點為A(1,m).過點B作AB的垂線BD,與反比例函數y=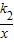 (x>0)的圖象交于點D(n,-2).
(x>0)的圖象交于點D(n,-2). 我市某海域內有一艘輪船發生故障,海事救援船接到求救信號后立即從港口出發沿直線勻速前往救援,與故障漁船會合后立即將其拖回.如圖折線段O-A-B表示救援船在整個航行過程中離港口的距離y(海里)隨航行時間x(分鐘)的變化規律.拋物線y=ax2+k表示故障漁船在漂移過程中離港口的距離y(海里)隨漂移時間x(分鐘)的變化規律.已知救援船返程速度是前往速度的
我市某海域內有一艘輪船發生故障,海事救援船接到求救信號后立即從港口出發沿直線勻速前往救援,與故障漁船會合后立即將其拖回.如圖折線段O-A-B表示救援船在整個航行過程中離港口的距離y(海里)隨航行時間x(分鐘)的變化規律.拋物線y=ax2+k表示故障漁船在漂移過程中離港口的距離y(海里)隨漂移時間x(分鐘)的變化規律.已知救援船返程速度是前往速度的 .根據圖象提供的信息,解答下列問題:
.根據圖象提供的信息,解答下列問題: 如圖,在平面直角坐標系中,O為坐標原點,點A、B的坐標分別為(8,0)、(0,6).動點Q從點O、動點P從點A同時出發,分別沿著OA方向、AB方向均以1個單位長度/秒的速度勻速運動,運動時間為t(秒)(0<t≤5).以P為圓心,PA長為半徑的⊙P與AB、OA的另一個交點分別為C、D,連接CD、QC.
如圖,在平面直角坐標系中,O為坐標原點,點A、B的坐標分別為(8,0)、(0,6).動點Q從點O、動點P從點A同時出發,分別沿著OA方向、AB方向均以1個單位長度/秒的速度勻速運動,運動時間為t(秒)(0<t≤5).以P為圓心,PA長為半徑的⊙P與AB、OA的另一個交點分別為C、D,連接CD、QC.