
科目: 來源: 題型:
手工課上,小明準備做一個形狀是菱形的風箏,這個菱形的兩條對角線長度之和恰好為![]() ,菱形的面積S(單位:
,菱形的面積S(單位:![]() )隨其中一條對角線的長
)隨其中一條對角線的長![]() (單位:
(單位:![]() )的變化而變化.
)的變化而變化.
(1)請直接寫出S與![]() 之間的函數關系式(不要求寫出自變量
之間的函數關系式(不要求寫出自變量![]() 的取值范圍);
的取值范圍);
(2)當![]() 是多少時,菱形風箏面積S最大?最大面積是多少?
是多少時,菱形風箏面積S最大?最大面積是多少?
(參考公式:當![]() ,函數
,函數![]() 有最小(大)值
有最小(大)值![]() )
)
查看答案和解析>>
科目: 來源: 題型:
王大伯幾年前承包了甲、乙兩片荒山,各栽100棵楊梅樹,成活98%.現已掛果,經濟效益初步顯現,為了分析收成情況,他分別從兩山上隨意各采摘了4棵樹上的楊梅,每棵的產量如折線統計圖所示.
(1)分別計算甲、乙兩山樣本的平均數,并估算出甲、乙兩山楊梅的產量總和;
(2)試通過計算說明,哪個山上的楊梅產量較穩定?
查看答案和解析>>
科目: 來源: 題型:
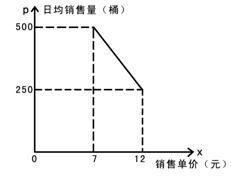
某桶裝水經營部每天的房租、人員工資等固定成本為250元,每桶水的進價是5元,規定銷售單價不得高于12元/桶,也不得低于7元/桶,調查發現日均銷售量p(桶)與銷售單價x(元)的函數圖象如圖所示.
(1)求日均銷售量p(桶)與銷售單價x(元)的函數關系;
(2)若該經營部希望日均獲利1350元,請你根據以上信息,就該桶裝水的銷售單價或銷售數量,提出一個用一元二次方程解決的問題,并寫出解答過程.
查看答案和解析>>
科目: 來源: 題型:
如圖,將□ABCD的邊DC延長到點E,使CE=DC,連接AE,交BC于點F.
(1)求證:△ABF≌△ECF;
(2)若∠AFC=2∠D,連接AC、BE.求證:四邊形ABEC是矩形.
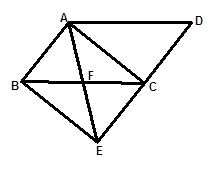
查看答案和解析>>
科目: 來源: 題型:
某課題學習小組在一次活動中對三角形的內接正方形的有關問題進行了探討:
定義:如果一個正方形的四個頂點都在一個三角形的邊上,那么我們就把這個正方形叫做三角形的內接正方形.
結論:在探討過程中,有三位同學得出如下結果:
甲同學:在鈍角、直角、不等邊銳角三角形中分別存在____個、____個、_____個大小不同的內接正方形.
乙同學:在直角三角形中,兩個頂點都在斜邊上的內接正方形的面積較大.
丙同學:在不等邊銳角三角形中,兩個頂點都在較大邊上的內接正方形的面積反而較小.
任務:(1)填充甲同學結論中的數據;
(2)乙同學的結果正確嗎?若不正確,請舉出一個反例并通過計算給予說明,若正確,請給出證明;
(3)請你結合(2)的判定,推測丙同學的結論是否正確,并證明。
(如圖,設銳角△ABC的三條邊分別為![]() 不妨設
不妨設![]() ,三條邊上的對應高分別為
,三條邊上的對應高分別為![]() ,內接正方形的邊長分別為
,內接正方形的邊長分別為![]() .若你對本小題證明有困難,可直接用“
.若你對本小題證明有困難,可直接用“![]() ”這個結論,但在證明正確的情況下扣1分).
”這個結論,但在證明正確的情況下扣1分).

查看答案和解析>>
科目: 來源: 題型:
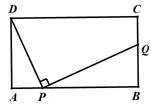
如圖,在矩形ABCD中,AD=4,AB=m(m>4),點P是AB邊上的任意一點(不與A、B重合),連結PD,過點P作PQ⊥PD,交直線BC于點Q.
(1)當m=10時,是否存在點P使得點Q與點C重合?若存在,求出此時AP的長;若不存在,說明理由;
(2)連結AC,若PQ∥AC,求線段BQ的長(用含m的代數式表示)
(3)若△PQD為等腰三角形,求以P、Q、C、D為頂點的四邊形的面積S與m之間的函數關系式,并寫出m的取值范圍.
查看答案和解析>>
科目: 來源: 題型:
如圖所示,四邊形OABC是矩形,點A、C的坐標分別為(3,0),
(0,1),點D是線段BC上的動點(與端點B、C不重合),過點D作直線
![]() =-
=-![]() +
+![]() 交折線OAB于點E.
交折線OAB于點E.
(1)記△ODE的面積為S,求S與![]() 的函數關系式;
的函數關系式;
(2)當點E在線段OA上時,若矩形OABC關于直線DE的對稱圖形為四邊形O1A1B1C1,試探究O1A1B1C1與矩形OABC的重疊部分的面積是否發生變化,若不變,求出該重疊部分的面積;若改變,請說明理由.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com