日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

如圖，有一直徑MN=4的半圓形紙片，其圓心為點P，從初始位置Ⅰ開始，在無滑動的情況下沿數軸向右翻滾至位置Ⅴ，其中，位置Ⅰ中的MN平行于數軸，且半⊙P與數軸相切于原點O；位置Ⅱ和位置Ⅳ中的MN垂直于數軸；位置Ⅲ中的MN在數軸上；位置Ⅴ中的點N到數軸的距離為3，且半⊙P與數軸相切于點A．

（1）紙片半⊙P從位置Ⅲ翻滾到位置Ⅳ時，點N所經過路徑長為            ;

（2）線段OA的長為            ．

（結果保留π）

（本題滿分6分）（1）計算：．

用配方法解方程：

（本題滿分8分）如圖，甲、乙兩個可以自由轉動的均勻的轉盤，甲轉盤被分成3個面積相等的扇形，乙轉盤被分成4個面積相等的扇形，每一個扇形都標有相應的數字，同時轉動兩個轉盤，當轉盤停止后，設甲轉盤中指針所指區域內的數字為m，乙轉盤中指針所指區域內的數字為n（若指針指在邊界線上時，重轉一次，直到指針都指向一個區域為止）．

（1）請你用畫樹狀圖或列表格的方法求出|m+n|＞1的概率；

（2）直接寫出點（m，n）落在函數圖象上的概率．

（本題滿分8分）丁丁想在一個矩形材料中剪出

如圖陰影所示的梯形，作為要制作的風箏的一個翅膀．

請你根據圖中的數據幫丁丁計算出BE、CD的長度

（結果精確到個位，）．

（本題滿分10分）如圖，一次函數y＝k₁x＋b的圖象經過

A（0，－2），B（1，0）兩點，與反比例函數的

圖象在第一象限內的交點為M，若△OBM的面積為2．

（1）求一次函數和反比例函數的表達式；

（2）在x軸上是否存在點P，使AM⊥MP？若存在，

求出點P的坐標；若不存在，說明理由．

（本題滿分10分）如圖，已知，以為直徑，為圓心的半圓交于點，點為弧CF的中點，連接交于點，為△ABC的角平分線，且，垂足為點.

（1）求證：是半圓的切線；

（2）若，，求的長.

（本題滿分12分） 小王家是新農村建設中涌現出的“養殖專業戶”．他準備購置80只相同規格的網箱，養殖A、B兩種淡水魚（兩種魚不能混養）．計劃用于養魚的總投資不少于7萬元，但不超過7.2萬元，其中購置網箱等基礎建設需要1.2萬元．設他用x只網箱養殖A種淡水魚，目前平均每只網箱養殖A、B兩種淡水魚所需投入及產業情況如下表：

（1）小王有哪幾種養殖方式？

（2）哪種養殖方案獲得的利潤最大？

（3）根據市場調查分析，當他的魚上市時，兩種魚的價格會有所變化，A種魚價格上漲a%（0＜a＜50），B種魚價格下降20%，考慮市場變化，哪種方案獲得的利潤最大？（利潤=收入-支出．收入指成品魚收益，支出包括基礎建設投入、魚苗投資及飼料支出）

（本題滿分12分）如圖，拋物線y＝a(x＋1)(x－5)與x軸的交點為M、N．直線y＝kx＋b

與x軸交于P(－2，0)，與y軸交于C．若A、B兩點在直線y＝kx＋b上，且AO=BO=，AO⊥BO．D為線段MN的中點，OH為Rt△OPC斜邊上的高．

(1)OH的長度等于___________；k＝___________，b＝____________；

(2)是否存在實數a，使得拋物線y＝a(x＋1)(x－5)上有一點E，滿足以D、N、E為頂

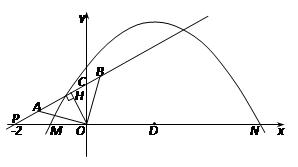點的三角形與△AOB相似?若不存在，說明理由；若存在，求所有符合條件的拋物線的解析式，同時探索所求得的拋物線上是否還有符合條件的E點(簡要說明理由)；并進一步探索對符合條件的每一個E點，直線NE與直線AB的交點G是否總滿足PB·PG＜，寫出探索過程．

下列各數中，最大的數是                                           （ ▲ ）

A.－1             B.0            C.1                  D.