
分析 根據題意①當m=0時,新的函數B的圖象剛好與直線y=x有3個不動點;②翻折后的部分與直線y=x有一個交點時,新的函數B的圖象剛好與直線y=x有3個不動點兩種情況求得即可.
解答 解:根據題意
①當m=0時,新的函數B的圖象剛好與直線y=-x有3個不動點;
②當m<0時,且翻折后的部分與直線y=-x有一個交點,
∵y=-$\frac{1}{2}$x2-4x=-$\frac{1}{2}$(x+4)2+8,
∴頂點為(-4,8),
∴在直線y=m上側的部分沿直線y=m翻折,翻折后的部分的頂點為(-4,-8-2m),
∴翻折后的部分的解析式為y=$\frac{1}{2}$(x+4)2-8-2m,
∵翻折后的部分與直線y=x有一個交點,
∴方程$\frac{1}{2}$(x+4)2-8-2m=x有兩個相等的根,
整理方程得x2+6x-4m=0.
∴△=36+16m=0,
解得m=-$\frac{9}{4}$,
綜上,滿足條件的m的值為0或-$\frac{9}{4}$.
故答案為:0或-$\frac{9}{4}$.
點評 本題考查了二次函數圖象與幾何變換,根據翻折的特征求得翻折后的部分的頂點坐標是解題的關鍵.


科目:初中數學 來源: 題型:填空題
 如圖,在矩形ABCD中,AD=4,AB=10,點E為邊DC上的一個動點(不與點D、C重合),把△ADE沿AE折疊,點D的對應點為點D′,若∠D′AB=30°,則DD′的長為4或4$\sqrt{3}$.
如圖,在矩形ABCD中,AD=4,AB=10,點E為邊DC上的一個動點(不與點D、C重合),把△ADE沿AE折疊,點D的對應點為點D′,若∠D′AB=30°,則DD′的長為4或4$\sqrt{3}$.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
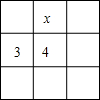 有這樣一個數字游戲:將1,2,3,4,5,6,7,8,9這九個數字分別填在如圖所示的九個空格中,要求每一行從左到右的數字逐漸增大,每一列從上到下的數字也逐漸增大.當數字3和4固定在圖中所示的位置時,x代表的數字是2,此時按游戲規則填寫空格,所有可能出現的結果共有6種.
有這樣一個數字游戲:將1,2,3,4,5,6,7,8,9這九個數字分別填在如圖所示的九個空格中,要求每一行從左到右的數字逐漸增大,每一列從上到下的數字也逐漸增大.當數字3和4固定在圖中所示的位置時,x代表的數字是2,此時按游戲規則填寫空格,所有可能出現的結果共有6種.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
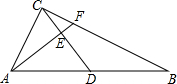 如圖,在△ABC中,∠ACB=90°,CD為AB邊上的中線,AE⊥CD于點E,交BC邊于點F,若AF=4,AB=8,則線段EF的長為$\frac{4}{5}$.
如圖,在△ABC中,∠ACB=90°,CD為AB邊上的中線,AE⊥CD于點E,交BC邊于點F,若AF=4,AB=8,則線段EF的長為$\frac{4}{5}$.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 31.63% | B. | 46.27% | C. | 53.73% | D. | 68.37% |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 兩點之間,線段最短 | B. | 兩點確定一條直線 | ||
| C. | 線段的中點定義 | D. | 直線可以向兩邊延長 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com