
【題目】已知一拋物線的頂點![]() 的坐標是
的坐標是![]() ,并且拋物線與
,并且拋物線與![]() 軸兩交點間的距離為
軸兩交點間的距離為![]() .
.
![]() 試求該拋物線的關系式;
試求該拋物線的關系式;
![]() 若點
若點![]() 在此拋物線上,且點
在此拋物線上,且點![]() 在第一象限,求以點
在第一象限,求以點![]() 、
、![]() 和坐標原點
和坐標原點![]() 為頂點的
為頂點的![]() 面積.
面積.
【答案】(1)拋物線的解析式為:![]() 或
或![]() ;(2)
;(2)![]() 面積是
面積是![]() .
.
【解析】
(1)已知了拋物線的對稱軸方程和拋物線與x軸兩交點間的距離,可求出拋物線與x軸兩交點的坐標;然后用待定系數法求出拋物線的解析式;
(2)根據(1)中的拋物線解析式得到點B的坐標,然后利用三角形的面積公式來求△OAB面積.
![]() ∵二次函數的頂點坐標
∵二次函數的頂點坐標![]() ,并且圖象與
,并且圖象與![]() 軸兩交點間距離為
軸兩交點間距離為![]() ,
,
∴二次函數圖象與![]() 軸兩交點坐標為
軸兩交點坐標為![]() 與
與![]() ,
,
設拋物線解析式為![]() ,
,
把![]() 代入,得
代入,得
![]() ,
,
解得![]() .
.
故拋物線的解析式為:![]() 或
或![]() .
.
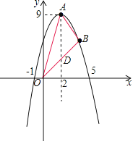
![]() 設直線
設直線![]() 與直線
與直線![]() 交于點
交于點![]() .
.
由![]() 知,拋物線的解析式為:
知,拋物線的解析式為:![]() .
.
把點![]() 代入,得
代入,得
![]() ,即
,即![]() ,
,
解得![]() ,
,![]() .
.
∵點![]() 在此拋物線上,且點
在此拋物線上,且點![]() 在第一象限,
在第一象限,
∴![]() .
.
易求直線![]() 的解析式為:
的解析式為:![]() .
.
把![]() 代入得到:
代入得到:![]() ,
,
∴![]() .
.
∴![]() ,即
,即![]() 面積是
面積是![]() .
.


科目:初中數學 來源: 題型:
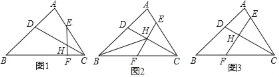
【題目】△ABC中,BC>AC,CD平分∠ACB交于AB于D,E,F分別是AC,BC邊上的兩點,EF交于CD于H,
(1)如圖1,若∠EFC=∠A,求證:CECD=CHBC;
(2)如圖2,若BH平分∠ABC,CE=CF,BF=3,AE=2,求EF的長;
(3)如圖3,若CE≠CF,∠CEF=∠B,∠ACB=60°,CH=5,CE=4![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】李紅在學校的研究性學習小組中負責了解初一年級200名女生擲實心球的測試成績.她從中隨機調查了若干名女生的測試成績(單位:米),并將統計結果繪制成了如下的統計圖表(內容不完整).
測試成績 |
|
|
|
|
| 合計 |
頻數 | 3 | 27 | 9 | m | 1 | n |

請你結合圖表中所提供的信息,回答下列問題:
(1)表中m= ,n= ;
(2)請補全頻數分布直方圖;
(3)在扇形統計圖中,![]() 這一組所占圓心角的度數為 度;
這一組所占圓心角的度數為 度;
(4)如果擲實心球的成績達到6米或6米以上為優秀,請你估計該校初一年級女生擲實心球的成績達到優秀的總人數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商場銷售一批名牌襯衫,平均每天可售出![]() 件,每件盈利
件,每件盈利![]() 元,為擴大銷售增加盈利,盡快減少庫存,商場決定采取適當的降價措施,經調查發現,如果每件襯衫每降價一元,市場每天可多售
元,為擴大銷售增加盈利,盡快減少庫存,商場決定采取適當的降價措施,經調查發現,如果每件襯衫每降價一元,市場每天可多售![]() 件,問他降價多少元時,才能使每天所賺的利潤最大?并求出最大利潤.
件,問他降價多少元時,才能使每天所賺的利潤最大?并求出最大利潤.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com