
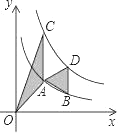
【題目】如圖,點A,B在反比例函數![]() (x>0)的圖象上,點C,D在反比例函數
(x>0)的圖象上,點C,D在反比例函數![]() (k>0)的圖象上,AC∥BD∥y軸,已知點A,B的橫坐標分別為1,2,△OAC與△ABD的面積之和為
(k>0)的圖象上,AC∥BD∥y軸,已知點A,B的橫坐標分別為1,2,△OAC與△ABD的面積之和為![]() ,則k的值為( )
,則k的值為( )
A. 3 B. 4 C. 2 D. ![]()
【答案】A
【解析】
先求出點A,B的坐標,再根據AC∥BD∥y軸,確定點C,點D的坐標,求出AC,BD,最后根據,△OAC與△ABD的面積之和為![]() ,即可解答.
,即可解答.
解:∵點A,B在反比例函數y=![]() (x>0)的圖象上,點A,B的橫坐標分別為1,2,
(x>0)的圖象上,點A,B的橫坐標分別為1,2,
∴點A的坐標為(1,1),點B的坐標為(2,![]() ),
),
∵AC∥BD∥y軸,
∴點C,D的橫坐標分別為1,2,
∵點C,D在反比例函數y=![]() (k>0)的圖象上,
(k>0)的圖象上,
∴點C的坐標為(1,k),點D的坐標為(2,![]() ),
),
∴AC=k-1,BD=![]()
![]() =
=![]() ,
,
∴S△OAC=![]() (k-1)×1=
(k-1)×1=![]() ,S△ABD=
,S△ABD=![]()
![]() ×(2-1)=
×(2-1)=![]() ,
,
∵△OAC與△ABD的面積之和為![]() ,
,
∴![]() +
+![]() =
=![]() ,
,
解得:k=3.
故選:A.


 開心蛙狀元測試卷系列答案
開心蛙狀元測試卷系列答案科目:初中數學 來源: 題型:
【題目】在⊙O中,AB為直徑,C為⊙O上一點.
(1)如圖①,過點C作⊙O的切線,與AB的延長線相交于點P,若∠CAB=28°,求∠P的大小;
(2)如圖②,D為弧AB上一點,且OD經過AC的中點E,連接DC并延長,與AB的延長線相交于點P,若∠CAB=10°,求∠P的大小.

查看答案和解析>>
科目:初中數學 來源: 題型:
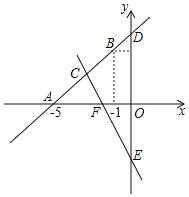
【題目】如圖,直線y=kx+b經過點A(-5,0),B(-1,4)
(1)求直線AB的表達式;
(2)求直線CE:y=-2x-4與直線AB及y軸圍成圖形的面積;
(3)根據圖象,直接寫出關于x的不等式kx+b>-2x-4的解集.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(本小題滿分7分) 已知:如圖,A是⊙O上一點,半徑OC的延長線與過點A的直線交于B點,OC=BC,AC=![]() OB.
OB.
(1)求證:AB是⊙O的切線;
(2)若∠ACD=45°,OC=2,求弦CD的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀下列兩段材料,回答問題:
材料一:A(x1.y1),B(x2.y2)的中點坐標為(![]() ,
,![]() ) 例如,點(1,5),(3,-1)的中點坐標為(
) 例如,點(1,5),(3,-1)的中點坐標為(![]() ,
,![]() ),即(2, 2)
),即(2, 2)
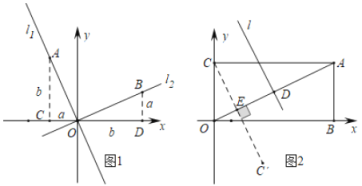
材料二:如圖1,正比例函數l1:y=k1x和l2:y=k2x的圖像相互垂直,分別在l1和l2上取點A、B,使得AO=BO.分別過點A、B作x軸的垂線,垂足分別為點C、D.顯然△AOC≌△ OBD.設OC=BD=a,AC=OD=b.則A(-a,b),B(b,a).于是![]() ,所以k1k2的值為一個常數.
,所以k1k2的值為一個常數.
(1)在材料二中,k1k2=____ (寫出這個常數具體的值) ;
(2)如圖,在矩形OBAC中A(4,2),點D是OA中點,用兩段材料的結論,求點D的坐標和OA的垂直平分線l的解析式;
(3)若點C’ 與點C關于OA對稱,用兩段材料的結論,求點C'的坐標,
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】班級元旦晚會上,主持人給大家帶來了一個有獎競猜題,他在一個不透明的袋子中放了若干個形狀大小完全相同的白球,想請大家想辦法估計出袋中白球的個數.數學課代表小明是這樣來估計的:他先往袋中放入10個形狀大小與白球相同的紅球,混勻后再從袋子中隨機摸出20個球,發現其中有4個紅球.如果設袋中有白球x個,根據小明的方法用來估計袋中白球個數的方程是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
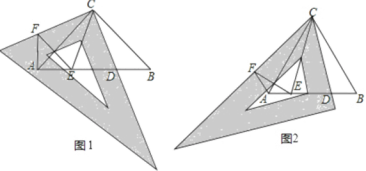
【題目】(1)如圖1,△ABC為等腰直角三角形,∠ACB=90°,先將三角板的90°角與∠ACB重合,再將三角板繞點C按順時針方向旋轉(旋轉角大于0°且小于45°).旋轉后三角板的一直角邊與AB交于點D.在三角板另一直角邊上取一點F,使CF=CD,線段AB上取點E,使∠DCE=45°,連接AF,EF.請探究結果:
①直接寫出∠EAF的度數=__________度;若旋轉角∠BCD=α°,則∠AEF=____________度(可以用含α的代數式表示);
②DE與EF相等嗎?請說明理由;
(類比探究)
(2)如圖2,△ABC為等邊三角形,先將三角板中的60°角與∠ACB重合,再將三角板繞點C按順時針方向旋轉(旋轉角大于0°且小于30°).旋轉后三角板的一直角邊與AB交于點D.在三角板斜邊上取一點F,使CF=CD,線段AB上取點E,使∠DCE=30°,連接AF,EF.
①直接寫出∠EAF的度數=___________度;
②若AE=1,BD=2,求線段DE的長度.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】直線l:y=﹣![]() x+6交y軸于點A,與x軸交于點B,過A、B兩點的拋物線m與x軸的另一個交點為C,(C在B的左邊),如果BC=5,求拋物線m的解析式,并根據函數圖像指出當m的函數值大于0的函數值時x的取值范圍.
x+6交y軸于點A,與x軸交于點B,過A、B兩點的拋物線m與x軸的另一個交點為C,(C在B的左邊),如果BC=5,求拋物線m的解析式,并根據函數圖像指出當m的函數值大于0的函數值時x的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com