
【題目】學校準備在各班設立圖書角以豐富同學們的課余文化生活.為了更合理的搭配各類書籍,學校團委以“我最喜愛的書籍”為主題,對學生最喜愛的一種書籍類型進行隨機抽樣調查,收集整理數據后,繪制出以下兩幅未完成的統計圖,請根據圖①和圖②提供的信息,解答下列問題:
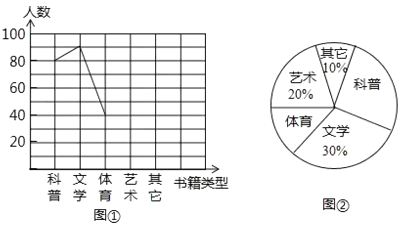
(1)在這次抽樣調查中,一共調查了_____________名學生;
(2)請把折線統計圖補充完整;
(3)在統計圖②中,求出“體育”部分所對應的圓心角的度數;
(4)若該校有學生2400人,估計喜歡“科普”書籍的有多少人?
【答案】(1)300名;(2)答案見解析;(3)48°;(4)640人.
【解析】
(1) 用最喜愛文字類的人數除以最喜愛文字類的所占百分比即可求解一共調查的學生的總人數即樣本總量;
(2)用最喜愛藝術類所占的百分比乘以參與調查的總人數求解最喜愛藝術類的總人數,用其它所占的百分比乘以調查人數的總人數求解其它的人數,根據所求補充折線統計圖即可;
(3)用最喜愛體育類所占的百分比乘以360°即可求出其所對應的圓心角的度數;
(4)由樣本估計總體可得,用最喜愛科普所占的百分比乘以該中學的學生總數即可求解.
(1):由第一個折線圖可以知道最喜愛文字類的人數為90人,
從第二個扇形圖可以知道最喜愛文字類的所占百分比是30%,
所以調查總人數:![]() (名),
(名),
因此,在這次抽樣調查中,一共調查了300名學生;
(2):由(1)知調查總人數是300,因此可得:
喜愛藝術的有:![]() (名),
(名),
喜愛其它的有:![]() (名)
(名)
補全的折線統計圖,如下圖所示:

(3):我們知道,圓所對應的圓心角是![]() ,
,
從圖1知道最喜愛體育的人數有40名,調查總人數是300名,
因此,“體育”部分所對應的圓心角的度數:![]() ,
,
答:在統計圖②中,“體育”部分所對應的圓心角的度數為![]() .
.
(4):從圖1的折線圖知道最喜愛科普的人數有80名,調查總人數的為300名,
所以該校喜歡“科普”書籍的大約有:![]() (人)
(人)
答:估計該校喜歡“科普”書籍的大約有640人.


科目:初中數學 來源: 題型:
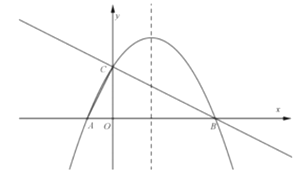
【題目】如圖,拋物線y=﹣2x2+8x﹣6與x軸交于點A、B,把拋物線在x軸及其上方的部分記作C1,將C1向右平移得C2,C2與x軸交于點B,D.若直線y=x+m與C1、C2共有3個不同的交點,則m的取值范圍是( )

A. ﹣2<m<![]() B. ﹣3<m<﹣
B. ﹣3<m<﹣![]() C. ﹣3<m<﹣2 D. ﹣3<m<﹣
C. ﹣3<m<﹣2 D. ﹣3<m<﹣![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系![]() 中,直線
中,直線![]() 與
與![]() 軸交于點
軸交于點![]() ,與
,與![]() 軸交于點
軸交于點![]() 拋物線
拋物線![]() 的對稱軸是直線
的對稱軸是直線![]() 與
與![]() 軸的交點為點
軸的交點為點![]() 且經過點
且經過點![]() 兩點.
兩點.
(1)求拋物線的解析式;
(2)點![]() 為拋物線對稱軸上一動點,當
為拋物線對稱軸上一動點,當![]() 的值最小時,請你求出點
的值最小時,請你求出點![]() 的坐標;
的坐標;
(3)拋物線上是否存在點![]() ,過點
,過點![]() 作
作![]() 軸于點
軸于點![]() 使得以點
使得以點![]() 為頂點的三角形與
為頂點的三角形與![]() 相似?若存在,請直接寫出點
相似?若存在,請直接寫出點![]() 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】仙桃是遂寧市某地的特色時令水果.仙桃一上市,水果店的老板用2400元購進一批仙桃,很快售完;老板又用3700元購進第二批仙桃,所購件數是第一批的![]() 倍,但進價比第一批每件多了5元.
倍,但進價比第一批每件多了5元.
(1)第一批仙桃每件進價是多少元?
(2)老板以每件225元的價格銷售第二批仙桃,售出80%后,為了盡快售完,剩下的決定打折促銷.要使得第二批仙桃的銷售利潤不少于440元,剩余的仙桃每件售價至少打幾折?(利潤=售價﹣進價)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】《孫子算經》是中國傳統數學最重要的著作,約成書于四、五世紀.現在傳本的《孫子算經》共三卷.卷上敘述算籌記數的縱橫相間制度和籌算乘除法則;卷中舉例說明籌算分數算法和籌算開平方法;卷下記錄算題,不但提供了答案,而且還給出了解法.其中記載:“今有木,不知長短.引繩度之,余繩四尺五,屈繩量之,不足一尺.問木長幾何?”
譯文:“用一根繩子去量一根長木,繩子還剩余4.5尺,將繩子對折再量長木,長木還剩余1尺,問長木長多少尺?”
請解答上述問題.
查看答案和解析>>
科目:初中數學 來源: 題型:
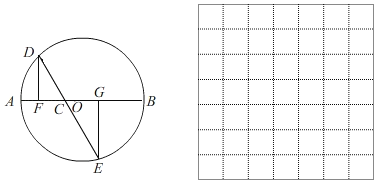
【題目】如圖,AB是⊙O的直徑,AB=4cm,C為AB上一動點,過點C的直線交⊙O于D、E兩點,且∠ACD=60°,DF⊥AB于點F,EG⊥AB于點G,當點C在AB上運動時,設AF=xcm,DE=ycm(當x的值為0或3時,y的值為2),探究函數y隨自變量x的變化而變化的規律.
(1)通過取點、畫圖、測量,得到了x與y的幾組對應值,如下表:
x/cm | 0 | 0.40 | 0.55 | 1.00 | 1.80 | 2.29 | 2.61 | 3 |
y/cm | 2 | 3.68 | 3.84 | 3.65 | 3.13 | 2.70 | 2 |
(2)建立平面直角坐標系,描出以補全后的表中各對對應值為坐標的點,畫出該函數的圖象;
(3)結合畫出的函數圖象,解決問題:點F與點O重合時,DE長度約為 cm(結果保留一位小數).
查看答案和解析>>
科目:初中數學 來源: 題型:
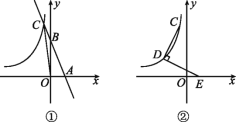
【題目】如圖①,直線y=-2x+4交x軸、y軸于A,B兩點,交雙曲線y=![]() (x<0)于C點,△OAC的面積為6.
(x<0)于C點,△OAC的面積為6.
(1)求雙曲線的解析式;
(2)如圖②,D為雙曲線y=![]() (x<0)上一點,連接CD,將線段CD繞點D順時針旋轉90°得線段DE,點E恰好落在x軸上,求點E的坐標.
(x<0)上一點,連接CD,將線段CD繞點D順時針旋轉90°得線段DE,點E恰好落在x軸上,求點E的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知開口向上的拋物線![]() 交
交![]() 軸于點
軸于點![]() ,
,![]() ,函數值
,函數值![]() 的最小值是
的最小值是![]() .
.
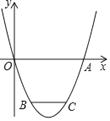
(1)求拋物線的解析式.
(2)點![]() 為拋物線上的點,并在對稱軸的左側.作
為拋物線上的點,并在對稱軸的左側.作![]() 軸交拋物線于點
軸交拋物線于點![]() ,連結
,連結![]() ,
,![]() ,且
,且![]() .
.
①求![]() 的值.
的值.
②若點![]() 在線段
在線段![]() 上,以點
上,以點![]() 為圓心,
為圓心,![]() 為半徑畫圓.當
為半徑畫圓.當![]() 和
和![]() 的一邊相切時,求點
的一邊相切時,求點![]() 的橫坐標.
的橫坐標.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com