設關于未知數x的方程x2-5x-m2+1=0的實根為α、β,試確定實數m的取值范圍,使|α|+|β|≤6成立.
【答案】
分析:根據x的方程x
2-5x-m
2+1=0的實根為α、β,由根與系數的關系列出不等式即可解出m的取值范圍.
解答:解:∵△=5
2+4(m
2-1)=4m
2+21,
∴不論m取何值,
所給的方程都有兩個不相等的實根.
∵α+β=5,αβ=1-m
2,|α|+|β|≤6,
∴α
2+β
2+2|αβ|≤36,
即(α+β)
2-2αβ+2|αβ|≤36.
∴25-2(1-m
2)+2|1-m
2|≤36,
當1-m
2≥0時,25≤36成立,
∴-1≤m≤1.(1)
當1-m
2<0時,
得25-4(1-m
2)≤36,
∴
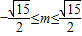
.(2)
由(1)、(2)得
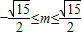
.
點評:本題考查了根與系數的關系,難度較大,關鍵是正確靈活運用根與系數的關系列出不等式.

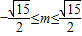 .(2)
.(2)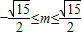 .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案