
【題目】A、B、C、D、E、F六個球隊進行單循環比賽(每兩隊之間賽一場,比賽結果必須分出勝負),每天同時在三個場地各進行一場比賽,前四天的積分表如下(E、F的積分被遮擋):
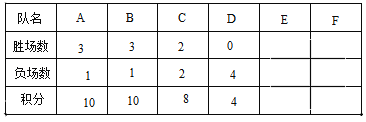
(1)根據積分榜,勝一場積幾分,負一場積幾分?
(2)若E隊前四天積分比F隊多4分,問E、F兩隊前四天的戰績分別是幾勝幾負?
(3)已知第一天B與D對陣,第二天C與E對陣,第三天D與F對陣,第四天B與C對陣,試分析第五天A和誰對陣比賽.
【答案】(1)勝一場積3分,負一場積1分;(2)E隊3勝1負,F隊1勝3負;(3)第五天A和B對陣比賽.
【解析】
(1)由D隊可知負一場積1分,設勝一場積x分,即能根據表格其他隊得分情況列方程求x的值.
(2)分別設E、F隊勝y場和z場,則負(4﹣y)場和(4﹣z)場,根據E對積分比F對多4分可列第一個方程;又前四天共打比賽3×4=12場,即所有隊伍勝的場數為12,可列得第二個方程.聯立方程組即能求y與z的值.
(3)條件里涉及B的比賽較多,可從B隊入手,第二天B不可能與C(第四天對陣)、D(第一天對陣)、E(本身當天有比賽)對陣,故只能與A或F對陣.利用反證法,假設第二天B與A對陣,即當天對陣情況為:A與B,C與E,D與F,但D與F是第三天才對陣,故出現矛盾,即第二天B不與A對陣而與F對陣.所以B要在第五天與A對陣,得答案.
解:(1)由D隊情況可得,負4場積4分
∴負一場得1分
設勝一場積x分,得:3x+1=10
解得:x=3
答:勝一場積3分,負一場積1分.
(2)設E隊勝y場,F隊勝z場,依題意得:
![]() 解得:
解得:![]() ,
,
答:E隊3勝1負,F隊1勝3負.
(3)由條件可知,第二天B與A或F對陣,
若第二天B與A對陣,即當天比賽是:B與A,C與E,D與F(與第三天才有D與F對陣矛盾),不成立
∴第二天B與F對陣,比賽為:C與E,B與F,A與D
∴第五天B與A對陣
答:第五天A和B對陣比賽.


 浙江新課程三維目標測評課時特訓系列答案
浙江新課程三維目標測評課時特訓系列答案 周周清檢測系列答案
周周清檢測系列答案 輕巧奪冠周測月考直通高考系列答案
輕巧奪冠周測月考直通高考系列答案科目:初中數學 來源: 題型:
【題目】育才中學開展了“孝敬父母,從家務事做起”活動,活動后期隨機調查了八年級部分學生一周在家做家務的時間,并將結果繪制成如下兩幅尚不完整的統計圖

請你根據統計圖提供的信息回答下列問題:
(1)本次調查的學生總數為 人,被調查學生做家務時間的中位數是 小時,眾數是 小時;
(2)請你補全條形統計圖;
(3)若全校八年級共有學生1500人,估計八年級一周做家務的時間為4小時的學生有多少人?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在矩形ABCD中,AB=8,BC=4,將矩形沿AC折疊,點D落在點D′處,則重疊部分△AFC的面積為( )

A.6B.8C.10D.12
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB與⊙O相切于點C,OA,OB分別交⊙O于點D,E, ![]() =
= ![]()

(1)求證:OA=OB;
(2)已知AB=4 ![]() ,OA=4,求陰影部分的面積.
,OA=4,求陰影部分的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB是⊙O的直徑,PB與⊙O相切于點B,連接PA交⊙O于點C,連接BC. 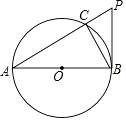
(1)求證:∠BAC=∠CBP;
(2)求證:PB2=PCPA;
(3)當AC=6,CP=3時,求sin∠PAB的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,BC=5,∠A=80°,∠B=70°,把△ABC沿RS的方向平移到△DEF的位置,若CF=4,則下列結論中錯誤的是( ) 
A.BE=4
B.∠F=30°
C.AB∥DE
D.DF=5
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:在Rt△ABC中,∠C=90°,BC=1,AC=![]() ,點D是斜邊AB的中點,點E是邊AC上一點,則DE+BE的最小值為( )
,點D是斜邊AB的中點,點E是邊AC上一點,則DE+BE的最小值為( )

A. 2
B. ![]()
C. ![]()
D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知四邊形ABCD是梯形,AD∥BC,∠A=90°,BC=BD,CE⊥BD,垂足為E. 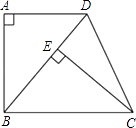
(1)求證:△ABD≌△ECB;
(2)若∠DBC=50°,求∠DCE的度數.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com