
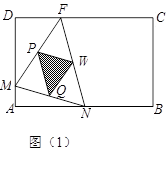
如圖(1),(2)所示,矩形ABCD的邊長(zhǎng)AB=6,BC=4,點(diǎn)F在DC上,DF=2。
動(dòng)點(diǎn)M、N分別從點(diǎn)D、B同時(shí)出發(fā),沿射線(xiàn)DA、線(xiàn)段BA向點(diǎn)A的方向運(yùn)動(dòng)(點(diǎn)M可
運(yùn)動(dòng)到DA的延長(zhǎng)線(xiàn)上),當(dāng)動(dòng)點(diǎn)N運(yùn)動(dòng)到點(diǎn)A時(shí),M、N兩點(diǎn)同時(shí)停止運(yùn)動(dòng)。連接FM、
FN,當(dāng)F、N、M不在同一直線(xiàn)時(shí),可得△FMN,過(guò)△FMN三邊的中點(diǎn)作△PQW。設(shè)動(dòng)點(diǎn)
M、N的速度都是1個(gè)單位/秒,M、N運(yùn)動(dòng)的時(shí)間為x秒。試解答下列問(wèn)題:
(1)說(shuō)明△FMN∽△QWP;
(2)設(shè)0≤x≤4(即M從D到A運(yùn)動(dòng)的時(shí)間段)。試問(wèn)x為何值時(shí),△PQW為直角三角形?
當(dāng)x在何范圍時(shí),△PQW不為直角三角形?
(3)問(wèn)當(dāng)x為何值時(shí),線(xiàn)段MN最短?求此時(shí)MN的值。
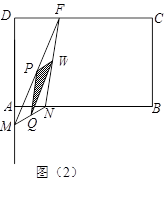
(1)提示:∵PQ∥FN,PW∥MN ∴∠QPW =∠PWF,∠PWF=∠MNF
∴∠QPW =∠MNF
同理可得:∠PQW =∠NFM或∠PWQ=∠NFM ∴△FMN∽△QWP
(2)當(dāng)![]() 時(shí),△PQW為直角三角形;
時(shí),△PQW為直角三角形;
當(dāng)0≤x<![]() ,
,![]() <x<4時(shí),△PQW不為直角三角形。(3)
<x<4時(shí),△PQW不為直角三角形。(3)![]()
解析:略



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
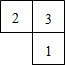 5、如圖是由幾個(gè)小立方塊所搭成的幾何體的俯視圖,小正方形體的數(shù)字表示該位置小立方塊的個(gè)數(shù),則該幾何體的主視圖是( )
5、如圖是由幾個(gè)小立方塊所搭成的幾何體的俯視圖,小正方形體的數(shù)字表示該位置小立方塊的個(gè)數(shù),則該幾何體的主視圖是( )查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
 如圖,已知數(shù)軸上A、B兩點(diǎn)所表示的數(shù)分別為-2和8.則線(xiàn)段AB的長(zhǎng)為( )
如圖,已知數(shù)軸上A、B兩點(diǎn)所表示的數(shù)分別為-2和8.則線(xiàn)段AB的長(zhǎng)為( )查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
 根據(jù)要求完成下面的填空:如圖,直線(xiàn)AB,CD被EF所截,若已知∠1=∠2.
根據(jù)要求完成下面的填空:如圖,直線(xiàn)AB,CD被EF所截,若已知∠1=∠2.查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話(huà):027-86699610 舉報(bào)郵箱:58377363@163.com