
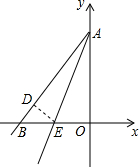
 已知如圖,直線AE:y=3x+12交x軸于E點,交y軸于A點,再把△AOE沿著AE翻折,使得AO落在AD的位置,設直線AD交軸x于點B,P點以1個單位每秒的速度自B點出發沿BO-OA向終點A運動,設點P的運動時間為t.
已知如圖,直線AE:y=3x+12交x軸于E點,交y軸于A點,再把△AOE沿著AE翻折,使得AO落在AD的位置,設直線AD交軸x于點B,P點以1個單位每秒的速度自B點出發沿BO-OA向終點A運動,設點P的運動時間為t. 時,求t的值,并判斷此時以P點為圓心,以
時,求t的值,并判斷此時以P點為圓心,以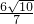 為半徑的圓與直線AE的位置關系.
為半徑的圓與直線AE的位置關系. =
=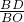 =
= =
=
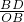 =
=
 =
=
 ,b=12
,b=12 x+12
x+12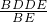 =
= =
=
 PE•DF=
PE•DF= (5-t)×
(5-t)× =-
=- t+6(0≤t<5)
t+6(0≤t<5)
 PE•DF=
PE•DF= (t-5)×
(t-5)× =
= t-6(5≤t<9)
t-6(5≤t<9)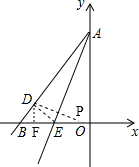
 x+12可知,當y=
x+12可知,當y= 時,x=-
時,x=- ,即點D的坐標為(-
,即點D的坐標為(- ,
, )
) ×OP•OE-
×OP•OE- ×AP•OF=48-
×AP•OF=48- (t-9)×4-
(t-9)×4- ×(21-t)×
×(21-t)× =
=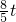 -
-
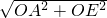 =4
=4
 =
=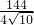 =
=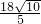 EN=AE-AN=4
EN=AE-AN=4 -
-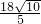 =
= ON=DN=
ON=DN= AN=
AN=
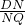 =
=
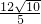

 PG
PG PG=
PG= PG
PG
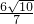 GE=
GE=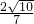
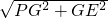 =
=
 即t=
即t=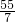
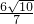
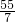 時,以P點為圓心,以
時,以P點為圓心,以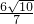 為半徑的圓與直線AE相切.
為半徑的圓與直線AE相切.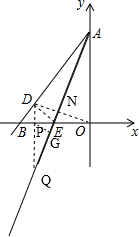



 即PM=
即PM=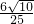

 PM=
PM=
 即t=
即t=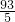
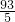 時,以P點為圓心,以
時,以P點為圓心,以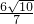 為半徑的圓與直線AE相交.
為半徑的圓與直線AE相交.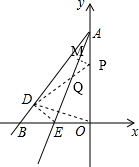
 x+12.
x+12. PE•DF,此時PE有兩種表示情況:①PE=5-t,②PE=t-5,所以可求出S的兩種情況,當點P在線段OA上時,△PDE的面積S=S四邊形ADEO-S△POE-S△ADP=2S△AOE-
PE•DF,此時PE有兩種表示情況:①PE=5-t,②PE=t-5,所以可求出S的兩種情況,當點P在線段OA上時,△PDE的面積S=S四邊形ADEO-S△POE-S△ADP=2S△AOE- ×OP•OE-
×OP•OE- ×AP•OF,此時OP=t-9,AP=OB+OA-t=21-t,代入即可求得S的第三種情況.
×AP•OF,此時OP=t-9,AP=OB+OA-t=21-t,代入即可求得S的第三種情況. ,可知tan∠DQN=
,可知tan∠DQN=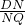 =
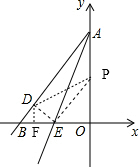
= ,滿足這個條件的點P有兩個,分別在直線AE的左右兩側.利用點D,O關于直線AE對稱,連接OD,可得AE⊥OD,DN=ON,AE=4
,滿足這個條件的點P有兩個,分別在直線AE的左右兩側.利用點D,O關于直線AE對稱,連接OD,可得AE⊥OD,DN=ON,AE=4 ,從而求出AN=
,從而求出AN=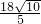 ,EN=AE-AN=
,EN=AE-AN= ,ON=
,ON= ,NQ=2DN=
,NQ=2DN=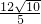 ,分兩種情況討論:①當點P在直線AE左側時,過點P做PG⊥AE于G,則QG=2PG,根據tan∠GPE=tan∠OAE=
,分兩種情況討論:①當點P在直線AE左側時,過點P做PG⊥AE于G,則QG=2PG,根據tan∠GPE=tan∠OAE= 求得t=
求得t=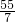 ,PG=
,PG=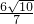 從而判斷以P點為圓心,以
從而判斷以P點為圓心,以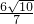 為半徑的圓與直線AE位置關系為相切.②當點P在直線AE右側時,過點P作PM⊥AE于點M根據tan∠MQP=tan∠DQN=
為半徑的圓與直線AE位置關系為相切.②當點P在直線AE右側時,過點P作PM⊥AE于點M根據tan∠MQP=tan∠DQN= ,tan∠PAM=
,tan∠PAM= 可求出PM=
可求出PM=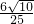 ,t=
,t=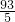 ,則可判斷以P點為圓心,以
,則可判斷以P點為圓心,以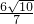 為半徑的圓與直線AE位置關系為相交.
為半徑的圓與直線AE位置關系為相交.

科目:初中數學 來源: 題型:
查看答案和解析>>
科目:初中數學 來源: 題型:
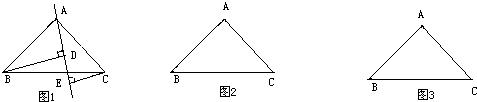
 已知如圖,直線AE:y=3x+12交x軸于E點,交y軸于A點,再把△AOE沿著AE翻折,使得AO落在AD的位置,設直線AD交軸x于點B,P點以1個單位每秒的速度自B點出發沿BO-OA向終點A運動,設點P的運動時間為t.
已知如圖,直線AE:y=3x+12交x軸于E點,交y軸于A點,再把△AOE沿著AE翻折,使得AO落在AD的位置,設直線AD交軸x于點B,P點以1個單位每秒的速度自B點出發沿BO-OA向終點A運動,設點P的運動時間為t.| 1 |
| 2 |
6
| ||
| 7 |
查看答案和解析>>
科目:初中數學 來源: 題型:
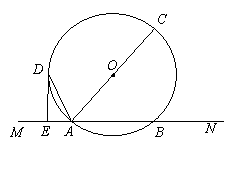
已知如圖,直線MN交⊙O于A、B兩點,AC是直徑,AD平分![]() CAM交⊙O于D,過D作DE
CAM交⊙O于D,過D作DE![]() MN于E.
MN于E.
(1)求證:DE是⊙O的切線;
(2)若DE=6cm,AE=3cm,求⊙O的半徑.
 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com