已知兩圓的半徑分別為5和12.當它們相切時,圓心距為 ;當圓心距等于13時,公共弦長為 .
【答案】
分析:分兩種情況考慮:當兩圓內切時,圓心距等于兩半徑相減;當兩圓外切時,圓心距等于兩半徑相加,根據已知的兩半徑即可求出相應的圓心距;當兩圓圓心距等于13時,根據13大于兩半徑之差,小于兩半徑之和,判斷得到兩圓相交,畫出相應的圖形,連接AE,BE,AF,BF,由AE=BE,AF=BF,根據線段垂直平分線的逆定理得到EF垂直平分AB,又AE=5,AF=12,EF=13,利用勾股定理的逆定理得到三角形AEF為直角三角形,利用面積法求出斜邊EF邊上的高AC的長,由AB=2AC即可得出公共弦AB的長.
解答:解:由兩圓的半徑分別為5和12,
當兩圓內切時,圓心距d=12-5=7;
當兩圓外切時,圓心距d=5+12=17,
當圓心距d=13時,∵12-5<d<12+5,
∴此時兩圓相交,畫出相應的圖形,如圖所示:
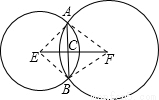
連接AE,AF,BE,BF,
則有AE=5,AF=12,即AE
2+AF
2=25+144=169,
又∵EF=13,即EF
2=169,
∴AE
2+AF
2=EF
2,
∴△AEF為直角三角形,
又AE=BE,AF=BF,
∴EF垂直平分AB,即AC⊥EF,AC=BC=

AB,
∵S
△AEF=

AE•AF=

EF•AC,
∴AC=
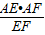
=
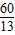
,
則AB=2AC=
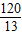
.
故答案為:7或17;
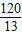 點評:
點評:此題考查了相切兩圓的性質,以及相交兩圓的性質,兩圓的位置關系可以由d,R,r的大小關系來判斷,當d<R-r時,兩圓內含;當d=R-r時,兩圓內切;當R-r<d<R+r時,兩圓相交;當d=R+r時,兩圓外切;當d>R+r時,兩圓外離,兩圓相交時,圓心距垂直平分兩圓的公共弦.


 AB,
AB, AE•AF=
AE•AF= EF•AC,
EF•AC,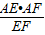 =
=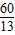 ,
,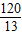 .
.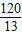


 閱讀快車系列答案
閱讀快車系列答案