
【題目】
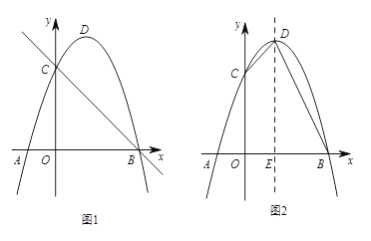
如圖1,拋物線![]() 與x軸交于點
與x軸交于點![]() 、點
、點![]() (點
(點![]() 在點
在點![]() 左側),與
左側),與![]() 軸交于點
軸交于點![]() ,點
,點![]() 為頂點,已知點
為頂點,已知點![]() 、點
、點![]() 的坐標分別為
的坐標分別為![]() 、
、![]() 。
。
(1)求拋物線的解析式;
(2)在直線![]() 上方的拋物線上找一點
上方的拋物線上找一點![]() ,使
,使![]() 的面積最大,求
的面積最大,求![]() 點坐標;
點坐標;
(3)如圖2,連結![]() 、
、![]() ,拋物線的對稱軸與x軸交于點
,拋物線的對稱軸與x軸交于點![]() 。過拋物線上一點
。過拋物線上一點![]() 作
作![]() ,交直線
,交直線![]() 于點
于點![]() ,求當
,求當![]() 時點
時點![]() 的坐標。
的坐標。
【答案】(1)拋物線的表達式為:![]() ;
;
(2)當![]() 時,S△BCD取最大值,此時P(
時,S△BCD取最大值,此時P(![]() ,
,![]() );
);
(3)點M坐標為(![]() ,
,![]() )或(
)或(![]() ).
).
【解析】試題分析:(1)把點A(-1,0)和點B(3,0)的坐標代入所給拋物線可得a、b的值,進而得到該拋物線的解析式;(2) )由題意設P(![]() ),過點P作x軸的垂線,交直線BC于點Q,再求得直線CB解析式,可得點Q的坐標,再求得PQ的長,利用S△BCD=
),過點P作x軸的垂線,交直線BC于點Q,再求得直線CB解析式,可得點Q的坐標,再求得PQ的長,利用S△BCD=![]() 得出以S、x為變量的二次函數模型,利用二次函數的性質求得x的值,即可得點P的坐標.(3)先求得點C,點E和頂點的坐標,再分當點M在對稱軸右側時和當點M在對稱軸左側時兩種情況求解即可.
得出以S、x為變量的二次函數模型,利用二次函數的性質求得x的值,即可得點P的坐標.(3)先求得點C,點E和頂點的坐標,再分當點M在對稱軸右側時和當點M在對稱軸左側時兩種情況求解即可.
試題解析:
解:(1)將A(-1,0)、B(3,0)兩點代入![]() 得:
得:
![]()
解得:![]()
∴拋物線的表達式為:![]()
(2)由題意設P(![]() ),過點P作x軸的垂線,交直線BC于點Q,
),過點P作x軸的垂線,交直線BC于點Q,
直線CB解析式:![]() , 則Q(
, 則Q(![]() )
)
∴PQ=![]()
S△BCD=![]()
∵![]() ,∴當
,∴當![]() 時,S△BCD取最大值,
時,S△BCD取最大值,
此時P(![]() )
)
(3)∵拋物線y=﹣(x﹣3)(x+1)=﹣x2+2x+3與與y軸交于點C,
∴C點坐標為(0,3),頂點(1,4),E(1,0)
∴tan∠BDE=![]()
(Ⅰ)當點M在對稱軸右側時.
i)若點N在射線CD上,
如圖,過點N作y軸的垂線,垂足為G,過點M作GN的垂線,垂足為H,
則△CNG,△MNH均為等腰直角三角形,
∵∠CMN=∠BDE,∴tan∠CMN = tan∠BDE![]()
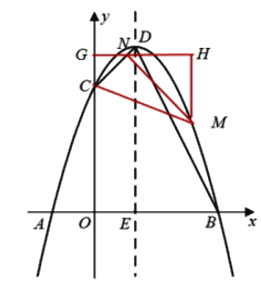
∴△CNG,△MNH相似比為1:2
設CG=a,則NG=a,NH=NH=2a,
∴M(3a,3+a-2a),即M(3a,3-a),
代入![]() 得:
得:
![]()
解得:![]()
此時M(![]() )
)
ii)若點N在射線DC上,
如圖,過點N作x軸的垂線l,分別過點M、C作GN的垂線,垂足為H、G,
則△CNG,△MNH均為等腰直角三角形,
∵∠CMN=∠BDE,∴tan∠CMN = tan∠BDE![]()
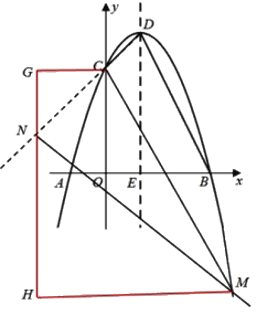
∴△CNG,△MNH相似比為1:2
設CG=a,則NG=a,NH=NH=2a,
∴M(a,3-a-2a),即M(a,3-3a),
代入![]() 得:
得:
![]()
解得:![]()
此時M(![]() )
)
(Ⅱ)當點M在對稱軸左側時.
∵∠CMN=∠BDE<45°,
∴∠MCN>45°,
而拋物線左側任意一點K,都有∠KCN<45°,
∴點M不存在.
綜上可知,點M坐標為(![]() ,
,![]() )或(
)或(![]() ).
).


科目:初中數學 來源: 題型:
【題目】在學校組織的游藝會上,投飛標游藝區游戲規則如下:如圖投到A區和B區的得分不同,A區為小圓內部分,B區為大圓內小圓外的部分(投中一次記一個點).現統計小華、小芳和小明投中與得分情況如下:
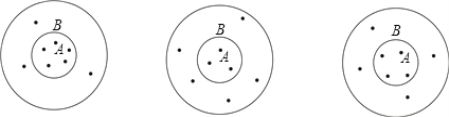
小華:90分 小芳86分 小明: ? 分
(1)求投中A區、B區一次各得多少分?
(2)依此方法計算小明的得分為多少分?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在兩個命題中,如果第一個命題的題設是第二個命題的結論,而第一個命題的結論是第二個命題的題設,那么這兩個命題叫做____________;如果把其中一個命題叫做原命題,那么另一個命題叫做它的____________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在△ABC中,a、b、c分別是∠A、∠B、∠C的對邊,
①若a2+b2>c2,則∠c為____________;
②若a2+b2=c2,則∠c為____________;
③若a2+b2<c2,則∠c為____________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知方程組 ![]() ,由于甲看錯了方程①中的a得到方程組的解為
,由于甲看錯了方程①中的a得到方程組的解為 ![]() ,乙看錯了方程②中的b得到方程組的解為
,乙看錯了方程②中的b得到方程組的解為 ![]() ,若按正確的a、b計算,則原方程組的解x與y的差x﹣y的值是多少?
,若按正確的a、b計算,則原方程組的解x與y的差x﹣y的值是多少?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com