
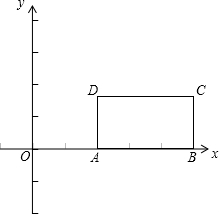
 已知:矩形ABCD(字母順序如圖)的邊長AB=3,AD=2,將此矩形放在平面直角坐標系xOy中,使AB在x軸正半軸上,而矩形的其它兩個頂點在第一象限,且直線y=
已知:矩形ABCD(字母順序如圖)的邊長AB=3,AD=2,將此矩形放在平面直角坐標系xOy中,使AB在x軸正半軸上,而矩形的其它兩個頂點在第一象限,且直線y= x-1經過這兩個頂點中的一個.
x-1經過這兩個頂點中的一個. x-1的上方?還是下方?還是正好落在此直線上?并說明理由.
x-1的上方?還是下方?還是正好落在此直線上?并說明理由.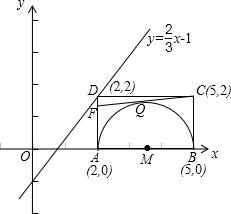 解:(1)如圖,建立平面直角坐標系,
解:(1)如圖,建立平面直角坐標系, x-1;則2=
x-1;則2= (m+3)-1,
(m+3)-1, x-1;
x-1; x-1,則2=
x-1,則2= m-1,m=2,
m-1,m=2, ,0),
,0),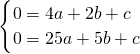 ,
,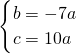 ,
, )2-
)2- a;
a; ,-
,- a)
a) <-
<- a<2,
a<2, <a<-
<a<- .
. ,
, )
) ;
; a=
a= ,
, ;
; x2+
x2+ x-5,
x-5, x-1與y軸交點(0,-1);
x-1與y軸交點(0,-1); x-1下方.
x-1下方. x-1與C點不過y=
x-1與C點不過y= x-1分析,即可求得矩形的頂點A、B、C、D的坐標;
x-1分析,即可求得矩形的頂點A、B、C、D的坐標; x-1下方.
x-1下方.

科目:初中數學 來源: 題型:
 已知:矩形ABCD,對角線AC、BD相交于點O.
已知:矩形ABCD,對角線AC、BD相交于點O.| BC |
| CD |
| AO |
| AD |
| AB |
| BC |
| BO |
查看答案和解析>>
科目:初中數學 來源: 題型:
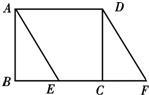 如圖,已知在矩形ABCD中,AB=3,點E在BC上且∠BAE=30°,延長BC到點F使CF=BE,連接DF.
如圖,已知在矩形ABCD中,AB=3,點E在BC上且∠BAE=30°,延長BC到點F使CF=BE,連接DF.查看答案和解析>>
科目:初中數學 來源: 題型:
 已知:矩形ABCD中AD>AB,O是對角線的交點,過O任作一直線分別交BC、AD于點M、N(如圖①).
已知:矩形ABCD中AD>AB,O是對角線的交點,過O任作一直線分別交BC、AD于點M、N(如圖①).| MN | DN |
查看答案和解析>>
科目:初中數學 來源: 題型:
| 10 | 7 |

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com